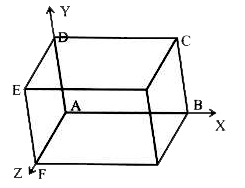
Consider a loop ABCDEFA. With coordinates A (0, 0, 0), B(5, 0, 0), C(5, 5, 0), D(0, 5, 0) E(0, 5, 5) and F(0, 0, 5). Find magnetic flux through loop due to magnetic field →B=3ˆi+4ˆk
The correct Answer is:175
To find the magnetic flux through the loop ABCDEFA due to the magnetic field →B=3^i+4^k, we will follow these steps:
Step 1: Identify the coordinates of the loop
The coordinates of the loop ABCDEFA are:
- A(0, 0, 0)
- B(5, 0, 0)
- C(5, 5, 0)
- D(0, 5, 0)
- E(0, 5, 5)
- F(0, 0, 5)
Step 2: Determine the area of the loop
The loop can be divided into two parts:
1. Loop ABCDA (in the xy-plane)
2. Loop ADEFA (in the yz-plane)
Area of loop ABCDA:
- This loop is a square with side length 5 m.
- Area AABCD=side2=5×5=25m2.
- The area vector →AABCD is perpendicular to the plane of the loop, which is along the z-axis:
→AABCD=25^km2
Area of loop ADEFA:
- This loop is also a square with side length 5 m.
- Area AADEFA=side2=5×5=25m2.
- The area vector →AADEFA is perpendicular to the plane of the loop, which is along the x-axis:
→AADEFA=25^im2
Step 3: Calculate the total area vector
The total area vector →A of the loop ABCDEFA is the sum of the area vectors of both loops:
→A=→AABCD+→AADEFA=25^k+25^i=25^i+25^km2
Step 4: Calculate the magnetic flux
Magnetic flux Φ through the loop is given by:
Φ=→B⋅→A
Substituting the values of →B and →A:
→B=3^i+4^k
→A=25^i+25^k
Now, calculating the dot product:
Φ=(3^i+4^k)⋅(25^i+25^k)=(3×25)+(4×25)=75+100=175Weber
Final Answer
The magnetic flux through the loop ABCDEFA due to the magnetic field →B is 175Weber.
---
The coordinates of the loop ABCDEFA are:
- A(0, 0, 0)
- B(5, 0, 0)
- C(5, 5, 0)
- D(0, 5, 0)
- E(0, 5, 5)
- F(0, 0, 5)
The loop can be divided into two parts:
1. Loop ABCDA (in the xy-plane)
2. Loop ADEFA (in the yz-plane)
- This loop is a square with side length 5 m.
- Area AABCD=side2=5×5=25m2.
- The area vector →AABCD is perpendicular to the plane of the loop, which is along the z-axis:
→AABCD=25^km2
- This loop is also a square with side length 5 m.
- Area AADEFA=side2=5×5=25m2.
- The area vector →AADEFA is perpendicular to the plane of the loop, which is along the x-axis:
→AADEFA=25^im2
The total area vector →A of the loop ABCDEFA is the sum of the area vectors of both loops:
→A=→AABCD+→AADEFA=25^k+25^i=25^i+25^km2
Magnetic flux Φ through the loop is given by:
Φ=→B⋅→A
Substituting the values of →B and →A:
→B=3^i+4^k
→A=25^i+25^k
Now, calculating the dot product:
Φ=(3^i+4^k)⋅(25^i+25^k)=(3×25)+(4×25)=75+100=175Weber
The magnetic flux through the loop ABCDEFA due to the magnetic field →B is 175Weber.
Similar Questions
A loop made of straight edges has six corners at A(0,0,0),B(L,O,0),C(L,L,0),D(0,L,0),E(0,L,L) and F(0,0,L). Where L is in meter. A magnetic field B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionA loop made of straight edegs has six corners at A(0,0,0),B(L,O,0)C(L,L,0),D(0,L,0)E(0,L,L) and F(0,0,L). Where L is in meter. A magnetic field B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionA loop made of straight edegs has six corners at A(0,0,0),B(L,O,0)C(L,L,0),D(0,L,0)E(0,L,L) and F(0,0,L). Where L is in meter. A magnetic field B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionA loop made of straight edegs has six corners at A(0,0,0),B(L,O,0)C(L,L,0),D(0,L,0)E(0,L,L) and F(0,0,L). Where L is in meter. A magnetic field B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionA loop A(0,0,0)B(5,0,0)C(5,5,0)D(0,5,0)E(0,5,10) and F(0,0,10) of straight edges has six corner points and two sides. The magnetic field in this region is →B=(3ˆi+4ˆk) T. The quantity of flux through the loop ABCDEFA (in Wb) is
View SolutionA loop A(0,0,0)B(5,0,0)C(5,5,0)D(0,5,0)E(0,5,10) and F(0,0,10) of straight edges has six corner points and two sides. The magnetic field in this region is →B=(3ˆi+4ˆk) T. The quantity of flux through the loop ABCDEFA (in Wb) is

View SolutionA loop ABCA of straight edges has three corner points A (8, 0, 0), B (0, 8, 0 ) and C (0, 0, 8). The magnetic field in this region is →B=5(ˆi+ˆj+ˆk)T0 . The quantity of flux through the loop ABCA (in Wb) is _____.
View SolutionA loop ABCA of straight edges has three corner points A (8, 0, 0), B (0, 8, 0 ) and C (0, 0, 8). The magnetic field in this region is →B=5(ˆi+ˆj+ˆk)T0 . The quantity of flux through the loop ABCA (in Wb) is _____.
View SolutionFind the radius of the sphere through the points (0,5,0),(4,3,0),(4,0,3)and(0,4,3)
View SolutionIf A=⎡⎢⎣234046589⎤⎥⎦ and B=⎡⎢⎣305532047⎤⎥⎦ , find 3A−2B .
View Solution
