Under an adiabatic process, the volume of an ideal gas gets doubled. Consequently the mean collision time between the gas molecule changes from to . If for this gas then a good estimate for is given by :
2
To solve the problem, let's break it down step by step.
Step 1: Understand the relationship between mean collision time and temperature and pressure.
The mean collision time τ is given by the formula:
τ=λVrms
where λ is the mean free path and Vrms is the root mean square speed of the gas molecules.
Step 2: Express mean free path and root mean square speed.
The mean free path λ can be expressed as:
λ=RT√2πD2NAP
And the root mean square speed Vrms is given by:
Vrms=√3RTm
Step 3: Substitute these into the equation for mean collision time.
Substituting the expressions for λ and Vrms into the formula for τ:
τ=RT√2πD2NAP√3RTm
This simplifies to:
τ∝RTP√3RT=R√TP√3
Thus, we can conclude that:
τ∝√TP
Step 4: Relate τ1 and τ2.
From the proportionality, we can write:
τ1τ2=√T1P1⋅P2√T2
This leads to:
τ1⋅P2P1=τ2⋅√T1√T2
Step 5: Use the adiabatic process relations.
In an adiabatic process, we have the relation:
T2T1=(V1V2)γ−1
Given that the volume doubles (V2=2V1), we can write:
T2T1=(12)γ−1
Step 6: Find the pressure ratio.
Using the ideal gas law and the adiabatic relations, we can also find:
P2P1=(V1V2)γ=(12)γ
Step 7: Substitute back into the equation for τ.
Now substituting these relations into our earlier equation:
τ1τ2=√T1T2⋅P2P1
Substituting the values we derived:
τ1τ2=
⎷T1(12)γ−1T1⋅(12)γ
This simplifies to:
τ1τ2=√2γ−1⋅(12)γ
Thus, we can express:
τ2τ1=2γ+122γ=21−γ2
Final Result
The final ratio of the mean collision times is:
τ2τ1=21+γ2
The mean collision time τ is given by the formula:
τ=λVrms
where λ is the mean free path and Vrms is the root mean square speed of the gas molecules.
The mean free path λ can be expressed as:
λ=RT√2πD2NAP
And the root mean square speed Vrms is given by:
Vrms=√3RTm
Substituting the expressions for λ and Vrms into the formula for τ:
τ=RT√2πD2NAP√3RTm
This simplifies to:
τ∝RTP√3RT=R√TP√3
Thus, we can conclude that:
τ∝√TP
From the proportionality, we can write:
τ1τ2=√T1P1⋅P2√T2
This leads to:
τ1⋅P2P1=τ2⋅√T1√T2
In an adiabatic process, we have the relation:
T2T1=(V1V2)γ−1
Given that the volume doubles (V2=2V1), we can write:
T2T1=(12)γ−1
Using the ideal gas law and the adiabatic relations, we can also find:
P2P1=(V1V2)γ=(12)γ
Now substituting these relations into our earlier equation:
τ1τ2=√T1T2⋅P2P1
Substituting the values we derived:
τ1τ2=
⎷T1(12)γ−1T1⋅(12)γ
This simplifies to:
τ1τ2=√2γ−1⋅(12)γ
Thus, we can express:
τ2τ1=2γ+122γ=21−γ2
The final ratio of the mean collision times is:
τ2τ1=21+γ2
Topper's Solved these Questions
Similar Questions
Knowledge Check
1 mole of an ideal gas at STP is subjected to a reversible adiabatic expansion to double its volume. Find the change in internal energy (γ=1.4)
A1169 JB769 JC1374 JD969 J
In an adiabatic process, volume is doubled then find the ratio of final average relaxation time & initial relaxation time. Given CpCv=γ
View SolutionThe temperature of an ideal gas undergoing adiabatic expansion varies with volume as T∝V−34, then the value of CPCV for the gas is
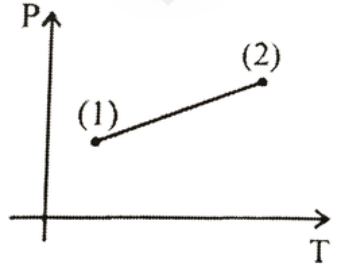
View SolutionFigure shows a process for a given amount of an ideal gas. If volume in state 1 is V1 & in state 2 is V2, then
View SolutionTemperature of an ideal gas is 300 K. The change in temperature of the gas when its volume changes from V to 2V in the process p = aV (Here, a is a positive constant) is
View SolutionTemperature of an ideal gas is 300 K . The final temperature of the gas when its volume changes from V to 2V in the process p=αV (here α is a positive constant) is
View SolutionProve that the pressure and the volume of a degenerate electron gas are related by an equation similar to the Poisson equation, and find the adiabatic index γ=Cp/Cv.
View SolutionConsider an ideal gas confined in an isolated closed chamber. As the gas undergoes an adiabatic expansion, the average time of collision between molecules increase as Vq, where V is the volume of the gas. The value of q is : (γ=CpCv)
View Solution