Normal at (2,2) to curve x2+2xy–3y2=0 is L. Then perpendicular distance from origin to line L is
2√2
2
4√2
√2
The correct Answer is:A
Step by step video & image solution for Normal at (2, 2) to curve x^2 + 2xy – 3y^2 = 0 is L. Then perpendicular distance from origin to line L is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE MAINBOOK - JEE MAINS PREVIOUS YEAR ENGLISHCHAPTER - JEE MAINEXERCISE - MATHEMATICS
121 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - JEE MAINS PREVIOUS YEAR ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions
2 Videos
- JEE MAINSBOOK - JEE MAINS PREVIOUS YEAR ENGLISHCHAPTER - JEE MAINSEXERCISE - All Questions
445 Videos
Similar Questions
The normal to the curve x2+2xy−3y2=0, at (1,1)
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionThe equation 3ax2+9xy+(a2−2)y2=0 represents two perpendicular straight lines for
View SolutionIf the straight lines joining origin to the points of intersection of the line x+y=1 with the curve x2+y2+x−2y−m=0 are perpendicular to each other , then the value of m should be
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
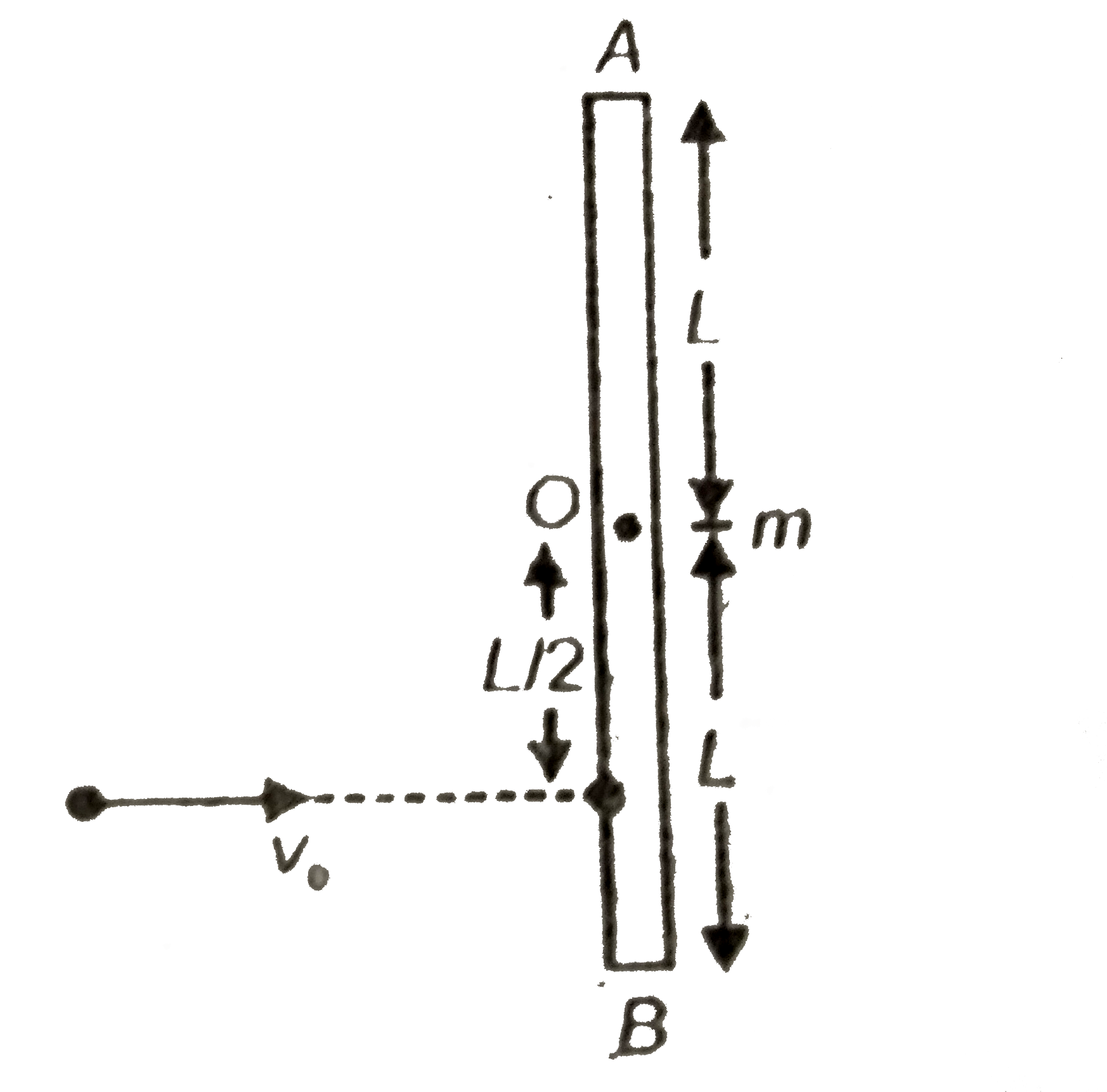
Distance of point P on rod from B which is at rest immediately afte collision is
View SolutionA straight line L at a distance of 4 units from the origin makes positive intercepts on the coordinate axes and the perpendicular from the origin to this line makes an angle of 60∘ with the line x+y=0. Then, an equation of the line L is
View SolutionReduce each of the equations to the normal form and find the length of the perpendicular from origin to the line x+y−2=0
View SolutionLet L1:x=y=zandL2=x−1=y−2=z−3 be two lines. The foot of perpendicular drawn from the origin O(0,0,0) on L1 to L2 is A. If the equation of a plane containing the line L1 and perpendicular to OA is 10x+by+cz=d, then the value of b+c+d is equal to
View SolutionThe normal at any point P(x1,y1) of curve is a line perpendicular to tangent at the point P(x1,y1). In case of rectangular hyperbola xy=c2, the equation of normal at (ct,ct) is xt3−yt−ct4+c=0. The shortest distance between any two curves always along the common normal.
If normal at (5, 3) of rectangular hyperbola xy−y−2x−2=0 intersect it again at a point:
View SolutionReduce each of the equations to the normal form and find the length of the perpendicular from origin to the line √3x+y+2=0
View Solution
