A beam of plane polarized light having flux 10−3 Watt falls normally on polarizer of cross sectional area 3×10−4m2. Polarizer rotates with angular frequency of 31.4 rad/s. Energy of light passes through the polarizer per revolution will be
10−4J
10−3J
10−2J
10−1J
The correct Answer is:A
To find the energy of light that passes through the polarizer per revolution, we can follow these steps:
Step 1: Understand the relationship between power, time, and energy.
The energy E passing through the polarizer can be calculated using the formula:
E=P×t
where P is the power of the light and t is the time duration for one complete revolution of the polarizer.
Step 2: Identify the given values.
From the problem statement, we have:
- Power P=10−3 Watts
- Angular frequency ω=31.4 rad/s
Step 3: Calculate the time period t of one revolution.
The time period T is given by the formula:
T=2πω
Substituting the value of ω:
T=2π31.4
Calculating this gives:
T≈6.2831.4≈0.2 seconds
Step 4: Calculate the energy E passing through the polarizer.
Now that we have the time period, we can substitute P and T into the energy formula:
E=P×T=10−3×0.2
Calculating this gives:
E=0.2×10−3=2×10−4 Joules
Step 5: Final answer.
Thus, the energy of light that passes through the polarizer per revolution is:
E=2×10−4 Joules
The energy E passing through the polarizer can be calculated using the formula:
E=P×t
where P is the power of the light and t is the time duration for one complete revolution of the polarizer.
From the problem statement, we have:
- Power P=10−3 Watts
- Angular frequency ω=31.4 rad/s
The time period T is given by the formula:
T=2πω
Substituting the value of ω:
T=2π31.4
Calculating this gives:
T≈6.2831.4≈0.2 seconds
Now that we have the time period, we can substitute P and T into the energy formula:
E=P×T=10−3×0.2
Calculating this gives:
E=0.2×10−3=2×10−4 Joules
Thus, the energy of light that passes through the polarizer per revolution is:
E=2×10−4 Joules
Topper's Solved these Questions
Similar Questions
A beam of plane polarised light of large cross - sectional area and uniform intensity of 3.3Wm−2 falls normally on a polariser (cross sectional are 3×10−4m2 ) which rotates about its axis with an angular speed of 31.4 rad/s . The energy of light passing through the polariser per revolution , is close to :
View SolutionIntensity of plane polarized light is 3.3 W/m. Area of plane 3x10−4m2 and polarizer rotates with 10π rad/sec. Energy transmitted in 1 complete cycle
View Solution
Knowledge Check
A solenoid of cross-sectional area 2×10−4m2 and 900 turns has 0.6Am2 magnetic moment. Then the current flowing through it is
A2.4AB2.34mAC3.33AD3.33mA
If 106 electrons/s are flowing through an area of cross section of 10−4m2 then the current will be:-
View SolutionTwo cylindrical vessels, each having length 10m and area of cross-sectional area of 1m2, are filled with water and rotated with angular speed ω=20rad/s. Then, which of the following statement is correct ?
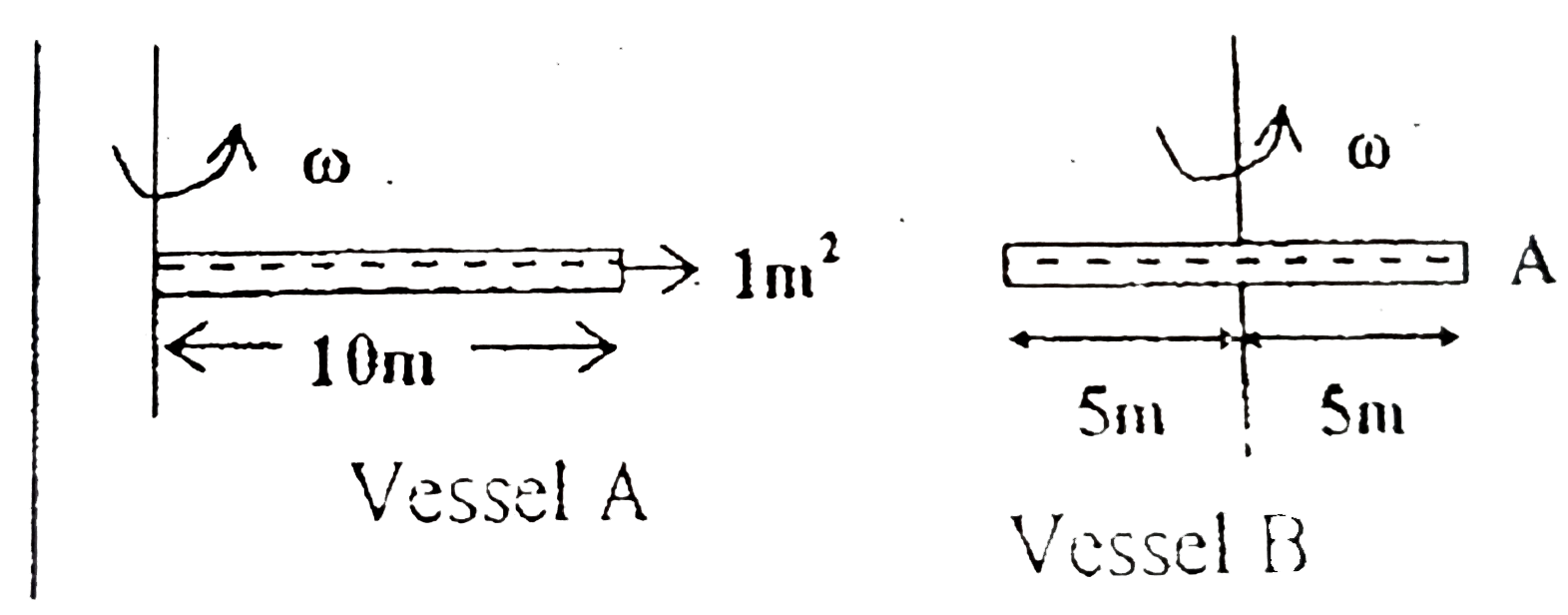
View SolutionA conducting wire of cross-sectional area 1cm2 has 3×1023 charge carriers per m3. If wire carries a current of 24mA, then drift velocity of carriers is
View SolutionA flywheel having a radius of gyration of 2m and mass 10 kg rotates at an angular speed of 5rads−1 about an axis perpendicular to it through its centre. The kinetic energy of rotation is
View SolutionA copper wire of cross - sectional area 3.4 mm2 and length of the wire 400m, specific resistivity of copper is 1.7×10−8Ω−m. Then the resistance of the wire is
View SolutionTwo beams A and B, of plane polarized light with mutually perpendicular planes of polarization are seen through a polaroid. From the position when the beam a has maximum intensity (and beam B has zero ntensity), a rotation of polaroid through 30∘ makes the two beams appear equally bright. If the initial intensities of the two beams are IA and IB respectively, then IAIB equals:
View SolutionThe horizontal component of earth's magnetic field is 3×10−5Wb/m2. The magnetic flux linked with a coil of area 1m2 and having 5 turns, whose plane is normal to the magnetic field, will be
View Solution
