Intensity of plane polarized light is 3.3 W/m. Area of plane 3x10−4m2 and polarizer rotates with 10π rad/sec. Energy transmitted in 1 complete cycle
4.95 x 10^(-4)
3.95 x 10^(-4)
2.95 x 10^(-4)
6.95 x 10^(-4)
The correct Answer is:A
To solve the problem, we need to calculate the energy transmitted through a rotating polarizer in one complete cycle. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the given parameters
- Intensity of plane polarized light (I): 3.3 W/m²
- Area of the plane (A): 3×10−4m2
- Angular velocity of the polarizer (ω): 10πrad/sec
Step 2: Determine the average transmitted intensity
The intensity of light transmitted through a polarizer is given by the formula:
I′=Icos2(θ)
where θ is the angle between the light's polarization direction and the axis of the polarizer.
Step 3: Calculate the average value of cos2(θ)
Since the polarizer rotates, θ changes with time. Over one complete cycle (from 0 to 2π), the average value of cos2(θ) can be calculated as:
⟨cos2(θ)⟩=12
Step 4: Calculate the average transmitted intensity
Now we can find the average transmitted intensity Iavg:
Iavg=I⋅⟨cos2(θ)⟩=3.3W/m2⋅12=1.65W/m2
Step 5: Calculate the energy transmitted in one complete cycle
The energy transmitted through the area A over one complete cycle can be calculated using the formula:
E=Iavg⋅A⋅T
where T is the time period of one complete cycle. The time period T can be calculated from the angular velocity:
T=2πω=2π10π=15sec
Now substituting the values:
E=Iavg⋅A⋅T=1.65W/m2⋅(3×10−4m2)⋅(15sec)
Step 6: Calculate the final energy
E=1.65⋅3×10−4⋅15=1.65⋅3⋅10−4⋅0.2=9.9×10−5J
Final Result
The energy transmitted in one complete cycle is:
E=9.9×10−5Jor4.95×10−5J
- Intensity of plane polarized light (I): 3.3 W/m²
- Area of the plane (A): 3×10−4m2
- Angular velocity of the polarizer (ω): 10πrad/sec
The intensity of light transmitted through a polarizer is given by the formula:
I′=Icos2(θ)
where θ is the angle between the light's polarization direction and the axis of the polarizer.
Since the polarizer rotates, θ changes with time. Over one complete cycle (from 0 to 2π), the average value of cos2(θ) can be calculated as:
⟨cos2(θ)⟩=12
Now we can find the average transmitted intensity Iavg:
Iavg=I⋅⟨cos2(θ)⟩=3.3W/m2⋅12=1.65W/m2
The energy transmitted through the area A over one complete cycle can be calculated using the formula:
E=Iavg⋅A⋅T
where T is the time period of one complete cycle. The time period T can be calculated from the angular velocity:
T=2πω=2π10π=15sec
E=Iavg⋅A⋅T=1.65W/m2⋅(3×10−4m2)⋅(15sec)
E=1.65⋅3×10−4⋅15=1.65⋅3⋅10−4⋅0.2=9.9×10−5J
The energy transmitted in one complete cycle is:
E=9.9×10−5Jor4.95×10−5J
Topper's Solved these Questions
Similar Questions
A beam of plane polarized light having flux 10−3 Watt falls normally on polarizer of cross sectional area 3×10−4m2. Polarizer rotates with angular frequency of 31.4 rad/s. Energy of light passes through the polarizer per revolution will be
View SolutionTerpinen - 4 - ol is an active ingredient in tea tree oil has the following structure
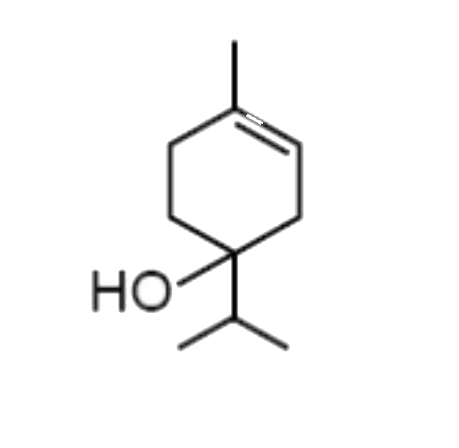
The correct observations for terpinen - 4 - ol is/are
I. It rotates the plane of plane polarized light.
II It does not rotates the plane of plane polarized light
III. On reaction with NaBranH2SO4 , it gives a di bromo compound
IV On ozonolysis it gives a compound with molecular formula C10H18O3.
View SolutionAn unpolarised light of intensity 64 Wm^(-2) passes through three polarisers such that the transmission axis of the last polariser is normal to first. If the intensity of emerging light is 6 Wm(-2),then angle between first two polariser may be
View Solution(a) When an unpolarized light of intensity I0 is passed through a polaroid , what is the intensity of the linearly polarized light ? Does it depend on the orintation of the polaroid ? Explain your answer.
(b) A plane polarized beam of light is passed through a polaroid . Show graphically the variation of the intensity of the transmitted light with angle of rotation of the polaroid in complete one rotation.
View SolutionA beam of plane polarised light of large cross - sectional area and uniform intensity of 3.3Wm−2 falls normally on a polariser (cross sectional are 3×10−4m2 ) which rotates about its axis with an angular speed of 31.4 rad/s . The energy of light passing through the polariser per revolution , is close to :
View SolutionThe intensity of a wave emitted from a small source at a distance 10 m is 20×10−3Wm−2. What is the intensity at a distance 100 m ?
View SolutionUnpolarized light of intensity I is incident on a system of two polarizers, A followed by B. The intensity of emergent light is I2. If a third polarizer C is placed between A and B, the intensity of emergent light is reduced to I3. The angle between the polarizers A and C is θ. Then :
View SolutionA large conducting plane has a surface charge density 1.0x10−4Cm−2 . Find the electrostatic energy stored in a cubical volume of edge 1 cm in the front plane.
View SolutionThe intensity of the sunlight reaching the earth is 1380 W(m^-2). Assume this light to be a plane, monochromatic wave. Find the amplitudes of electric and magnetic field in this wave.
View SolutionA solid cylinder rolls down an inclined plane of height 3m and reaches the bottom of plane with angular velocity of 2√2rad/s. The radius of cylinder must be [take g=10m/s2]
View Solution
