Bus moving with speed v forwards a stationary wall. it produces sound of frequency f=420Hz.Theheardequencyofref≤ctedsoundomwallbydriveris490 Hz.Calca––tethespeedvofbus.Thevelocityofsound∈airis330 m/s.
61Kms
71 Km/s
81Kms
91Kms
The correct Answer is:D
To solve the problem, we can use the Doppler effect formula for sound. The situation involves a moving source (the bus) and a stationary observer (the wall). The steps to find the speed of the bus are as follows:
Step 1: Understand the given values
- Frequency of sound produced by the bus (f1) = 420 Hz
- Frequency of sound heard by the driver after reflection (f2) = 490 Hz
- Velocity of sound in air (c) = 330 m/s
Step 2: Set up the Doppler effect equations
When the bus is moving towards the wall, the frequency of the sound heard by the wall (f1) is given by:
f1=f(cc−v)
Where:
- f is the original frequency (420 Hz)
- v is the speed of the bus
When the sound reflects off the wall and travels back to the bus, the frequency heard by the driver (f2) is given by:
f2=f1(c+vc)
Step 3: Substitute the known values
From the first equation:
420=f(330330−v)
From the second equation:
490=420(330+v330)
Step 4: Solve the second equation for v
Rearranging the second equation:
490=420(330+v330)
490420=330+v330
4942=330+v330
Cross-multiplying gives:
49⋅330=42⋅(330+v)
Step 5: Expand and simplify
Expanding the equation:
16170=13860+42v
Rearranging gives:
16170−13860=42v
2310=42v
v=231042
v=55 m/s
Step 6: Convert to km/h
To convert the speed from m/s to km/h:
vkm/h=vm/s×185
vkm/h=55×185=198 km/h
Final Answer
The speed of the bus is approximately 198 km/h.
---
- Frequency of sound produced by the bus (f1) = 420 Hz
- Frequency of sound heard by the driver after reflection (f2) = 490 Hz
- Velocity of sound in air (c) = 330 m/s
When the bus is moving towards the wall, the frequency of the sound heard by the wall (f1) is given by:
f1=f(cc−v)
Where:
- f is the original frequency (420 Hz)
- v is the speed of the bus
f2=f1(c+vc)
From the first equation:
420=f(330330−v)
490=420(330+v330)
Rearranging the second equation:
490=420(330+v330)
490420=330+v330
4942=330+v330
Cross-multiplying gives:
49⋅330=42⋅(330+v)
Expanding the equation:
16170=13860+42v
Rearranging gives:
16170−13860=42v
2310=42v
v=231042
v=55 m/s
To convert the speed from m/s to km/h:
vkm/h=vm/s×185
vkm/h=55×185=198 km/h
The speed of the bus is approximately 198 km/h.
Topper's Solved these Questions
Similar Questions
A car is moving towards a fixed wall, it blows form of frequency of 440Hz . The frequency of reflected sound observed by the driver is 480Hz then find the speed of car in km/hr. (Speed of sound is 350msec
View Solutiona bus is moving towards and stationary observer with speed 20 m/s blows a horn of frequency 200 Hz. the frequency of sound heard by the observer is approximately ( take speed of sound 320 m/s)
View SolutionA train is moving with speed 72 km/h towards a hill blows a whistle of frequency 1240Hz. the frequency of echo heard by driver is(speed of sound=330m/s)
View SolutionA car travels at a speed of 'a' towards a high wall. The driver sounds a horn of frequency 'n'. If V is the velocity of sound in air, frequency of reflected sound heard by the driver is
View Solution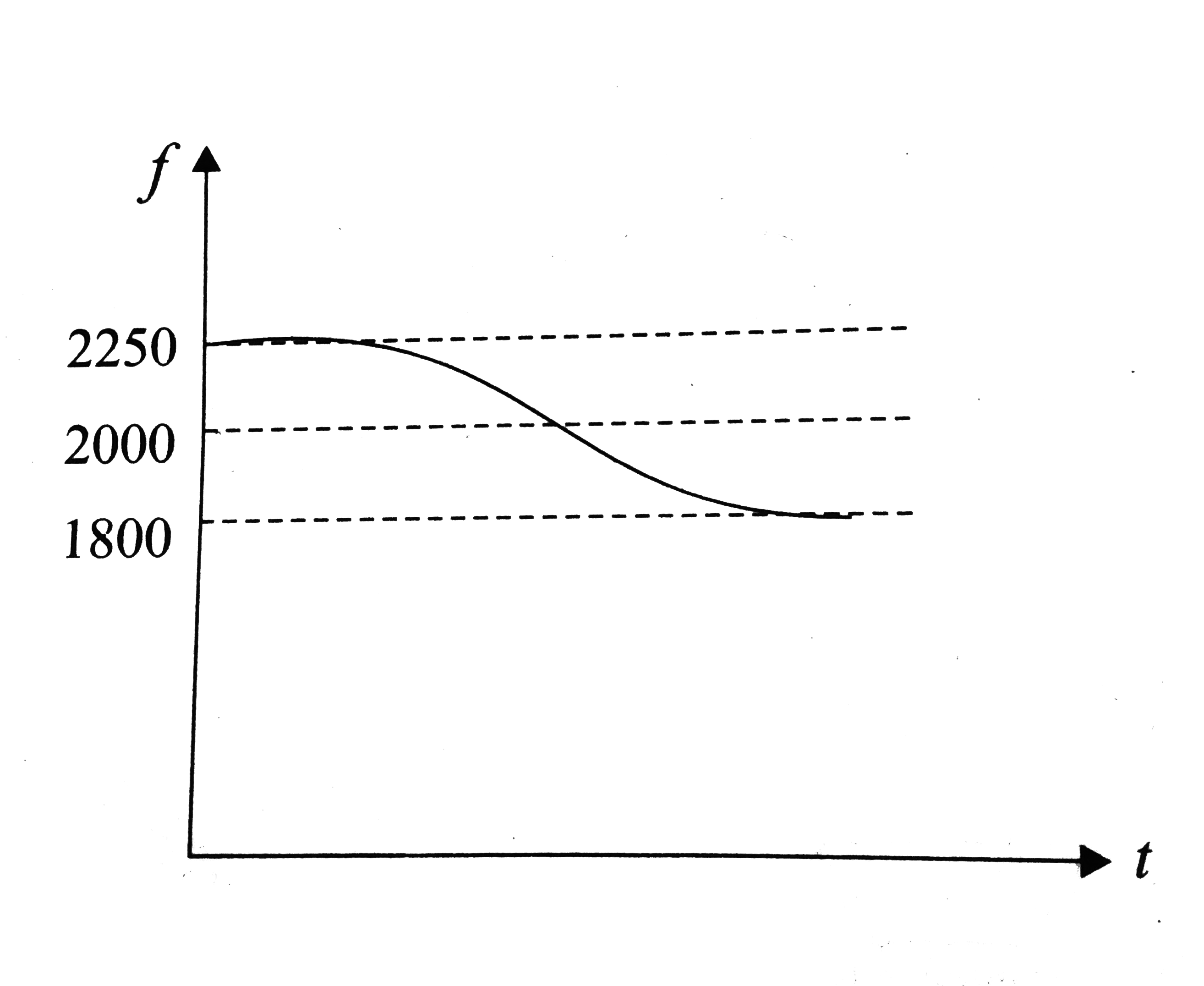
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300ms
View SolutionA source emits sound of frequency 600Hz inside water. The frequency heard in air will be equal to (velocity of sound in water=1500ms, velocity of sound in air=300(m)/(s))
View SolutionAn observer is moving towards a source with speed 15 m/s. The source is moving with speed 5 m/s in the same direction. Air is blowing with speed 10 m/s from observer to source. If frequency of sound emitted is 325 Hz then find frequency of sound heard by observer (velocity of sound in air = 330 m/s) in Hz .
View SolutionThe driver of a car travelling with speed 30ms−1 towards a hill sounds a horn of frequency 600 Hz. If the velocity of sound in air is 330ms−1, the frequency of reflected sound as heard by driver is
View SolutionA car emitting sound of frequency 500 Hz speeds towards a fixed wall at 4ms. An observer in the car hears both the source frequency as well as the frequency of sound reflected from the wall. If he hears 10 beats per second between the two sounds, the velocity of sound in air will be
View SolutionA car is moving with a constant velocity 10m/s towards the stationary wall. The car blows a horn of frequency 320Hz. The velocity of sound in air is 330m/s. The beats frequency received by the observer is

View Solution