For the equilibrium A⇔B , the variation of the rate of the forward (a) and reverse (b) reaction with time is given by :
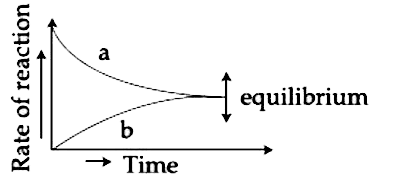

The correct Answer is:A
To solve the problem regarding the equilibrium of the reaction A⇌B and the variation of the rates of the forward and reverse reactions with time, we can follow these steps:
1. Understand the Reaction Dynamics:
- The reaction A⇌B involves the conversion of reactant A into product B and vice versa.
- Initially, the concentration of reactants (A) is higher than that of products (B).
Hint: Consider how the concentrations of reactants and products change over time.
2. Rate of Forward and Reverse Reactions:
- The rate of the forward reaction is proportional to the concentration of reactants:
Rateforward=kf(A)
- The rate of the reverse reaction is proportional to the concentration of products:
Ratereverse=kr(B)
Hint: Remember that the rates depend on the concentrations of the respective species involved in the reaction.
3. Initial Conditions:
- At the beginning of the reaction, since (A) is greater than (B), the rate of the forward reaction will be greater than that of the reverse reaction.
- This means that the forward reaction will dominate initially, leading to a decrease in (A) and an increase in (B).
Hint: Think about how the reaction progresses and how the concentrations change over time.
4. Approaching Equilibrium:
- As the reaction proceeds, the concentration of A decreases while the concentration of B increases.
- Eventually, the concentrations will reach a point where the rate of the forward reaction equals the rate of the reverse reaction.
Hint: Consider what happens to the rates as the concentrations approach a balance.
5. Equilibrium Condition:
- At equilibrium, the rates of the forward and reverse reactions are equal:
kf(A)=kr(B)
- This indicates that the system has reached a state where the concentrations of A and B remain constant over time.
Hint: Recall the definition of chemical equilibrium and how it is characterized by constant concentrations.
6. Conclusion:
- The correct interpretation of the variation of rates with time indicates that the forward reaction rate decreases while the reverse reaction rate increases until they become equal at equilibrium.
Final Answer:
The best option that describes the variation of the rates of the forward and reverse reactions with time is that initially, the forward reaction rate is greater than the reverse reaction rate, and at equilibrium, both rates are equal.
- The reaction A⇌B involves the conversion of reactant A into product B and vice versa.
- Initially, the concentration of reactants (A) is higher than that of products (B).
- The rate of the forward reaction is proportional to the concentration of reactants:
Rateforward=kf(A)
- The rate of the reverse reaction is proportional to the concentration of products:
Ratereverse=kr(B)
- At the beginning of the reaction, since (A) is greater than (B), the rate of the forward reaction will be greater than that of the reverse reaction.
- This means that the forward reaction will dominate initially, leading to a decrease in (A) and an increase in (B).
- As the reaction proceeds, the concentration of A decreases while the concentration of B increases.
- Eventually, the concentrations will reach a point where the rate of the forward reaction equals the rate of the reverse reaction.
- At equilibrium, the rates of the forward and reverse reactions are equal:
kf(A)=kr(B)
- This indicates that the system has reached a state where the concentrations of A and B remain constant over time.
- The correct interpretation of the variation of rates with time indicates that the forward reaction rate decreases while the reverse reaction rate increases until they become equal at equilibrium.
The best option that describes the variation of the rates of the forward and reverse reactions with time is that initially, the forward reaction rate is greater than the reverse reaction rate, and at equilibrium, both rates are equal.
Topper's Solved these Questions
Similar Questions
For the equilibrium,
A(g)→B(g),ΔH is -40 KJ/mol.
If the ratio of the activation energies of the forward (Ef) and reverse (Eb) reactions is 23 then:
View SolutionA reaction having equal energies of activation for forward and reverse reactions has
View SolutionA reaction having equal energies of activation for forward and reverse reactions has
View SolutionFor the reversible reaction,A+B⇔C, the specific reaction rates for forward and reverse reactions are 1.25×103and2.75×104 respectively. The equilibrium constant for the reaction is:
View SolutionThe free energy change for a reversible reaction at equilibrium is
View SolutionMass action rato or reaction quotient Q for a reaction can be calculate using the law of masss action
A(g)+B(g)⇔C(g)+D(g)
Q=[C][D][A][B]
The value of Q decides whether the reaction is at equilibrium or not.
At equilibrium, Q=K
For an equilibrium process, Q≠K
when Q>K, reaction will favour backward direction and when Q<K, it will favour direction.
Answer the following questions:
In the reaction:
NH4Cl(g)⇔NH3(g)+HCl(g)
a graph is plotted to show that the variation or the rate of forward and backward reaction against time.
Which of following is correct?
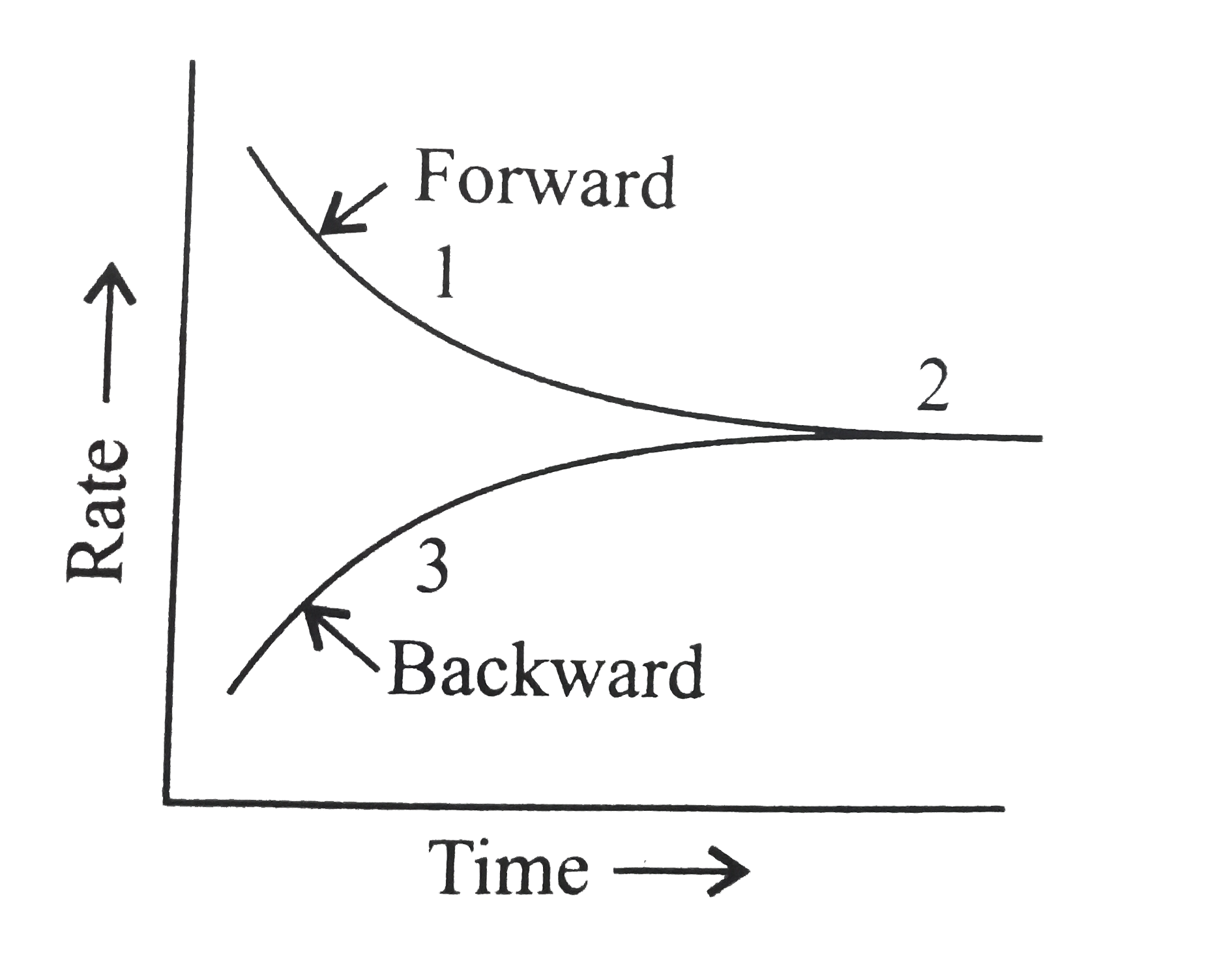
View SolutionFor the reaction A+B⇔C, the rate constants for the forward and the reverse reactions are 4×102 and 2×102 respectively. The value of equilibrium constant K for the reaction would be
View SolutionDraw a representative reaction curve for an exothermic reaction and (i) label the activation energies for the forward and reverse reaction (ii) enthalpy for the forward and reverse reactions. How will the curve change with the addition of a catalyst ?
View SolutionFor an equilibrium reaction, the rate constants for the forward and the backward reaction are 2.38×10−4 and 8.15×10−5, respectively. Calculate the equilibrium constant for the reaction.
View SolutionFor the physical equilibrium ice ⇔ water, the forward reaction is not favoured by
View Solution
