The cirtical angular velocity ωc of a cylinder inside another cylinder containing a liquied at which its turbulance occurs depends on visocisity η density ρ and disntac d between wall of the cylinder. Obtain an expression for ωc using method of dimensios.
Step by step video & image solution for The cirtical angular velocity omega_c of a cylinder inside another cylinder containing a liquied at which its turbulance occurs depends on visocisity eta density rho and disntac d between wall of the cylinder. Obtain an expression for omega_c using method of dimensios. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
The critical angular velocity ωc of a cylinder inside another cylinder containing a liquid at which its turbulence occurs depends on viscosity η, density ρ and the distance d between the walls of the cylinders . Find an expression for ωc.
View SolutionA gas fills up the space between two long coaxial cylinders of radii R1 and R2, with R1<R2. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. The moment of friction forces acting on a unit length of the inner cylinder is equal to N1. Find the viscosity coefficient η of the gas taking into account that the friction force acting on a unit area of the cylindrical surface of radius r is determined by the formule σ=ηr(∂ω/∂r).
View Solution
Knowledge Check
- Question 1 - Select One
A person stands in contact against the inner surface of a cylindrical drum of radius (R ) rotating with angular velocity ω . The coefficient of friction between the inner surface of the minumum rotational speed of the cylinder , which enables the person to ramain stuck to the wall , when the platform on which the person was standing is suddenly removed ?
A√μRgB√gμRC√2gμRD√rgμ
An infinite cylinder of radius r with surface charge density σ is rotated about its central axis with angular speed ω. Then the magnetic field at any point inside the cylinder is
View SolutionA cylinder of mass M, radius r1 and lenglth l is kept inside another cylinder of radius r2 and length l. The space between them is filled with a liquid of viscosity η. The inner cylinder starts rotating with angular velocity ω while the other cylinder is at rest. Find time when inner cylinder stops.
View SolutionA string is wrapped around a cylinder of mass M and radius r. The string is pulled vertically upward to prevent the center of mass from falling as the cylinder unwinds the string. (a) What is the tension in the string? B) How much work has been done on the cylinder once it has reached an angular speed ω? c) what is the length of string unwound in the time its acquires angular speed ω?
View SolutionA metal rod OA of mann 'm' and length 'r' is kept rotating with a constantangular speed ω in a vertical plane about a horizontal axis at the end O. The free end A is arraged to slide without friction along fixed conduction circular ring in the same plane as that of rotation. A uniform and constant magnetic induction →B is applied perpendicular and into the plane of rotation as shown in the figure below. An inductor L and an external resistance R are connected through a swithch S between the point O and a point C on the ring to form an electrical circuit. Neglect the resistance of the ring and the rod. Initially, the switch is open.
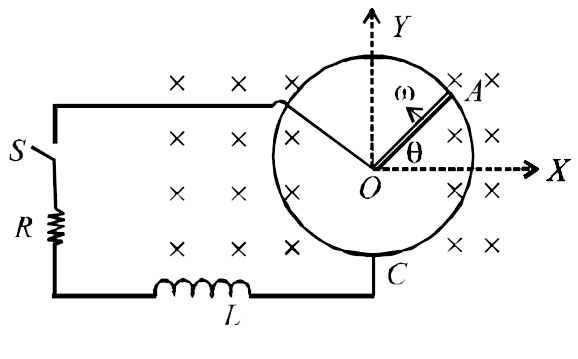
(a) What is the induced emf across the teminal of the switch?
(b) The switch S is closed at time t=0.
(i) Obtain an expression for the current as a function of time.
(ii) In the steady state, obtin the time dependence of the torque required to maintain the constant angular speed, given that the rod OA was along th positive X-axis at t=0.View SolutionA cylinder rotating with angular velocity ω0 is put on a rough horizontal floor so that edge touches a vertical rough wall. Rotational motion of the cylinder is retarded and after some time cylinder comes to rest. If m is mass of cylinder and R is its radius then calculate number of revolutions made by the cylinder before it comes to rest. Assume μ is coefficient of friction for floor as well as wall.
View SolutionA uniform solid cylinder of mass m and radius R is set in rotation about its axis with an angular velocity ω0, then lowered with its lateral surface onto a horizontal plane and released. The coefficient of friction between the cylinder and the plane is equal to μ. Find
(a) how long the cylinder will move with sliding,
(b) the total work performed by the sliding friction force acting on the cylinder.View SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R2 with its center on the axis of the cylinder, as shown in the figure. The magnitude of the electric field at the point P, which at a distance 2 R (from the axis of the cylinder, is given by the expression 23ρR16nɛ0, The value of n is
'(##CEN_KSR_PHY_JEE_C18_E01_040_Q24##)'View Solution

