The critical angular velocity ωc of a cylinder inside another cylinder containing a liquid at which its turbulence occurs depends on viscosity η, density ρ and the distance d between the walls of the cylinders . Find an expression for ωc.
The correct Answer is:ωc=kη/ρd2
Step by step video, text & image solution for The critical angular velocity omega_c of a cylinder inside another cylinder containing a liquid at which its turbulence occurs depends on viscosity eta, density rho and the distance d between the walls of the cylinders . Find an expression for omega_c. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The cirtical angular velocity ωc of a cylinder inside another cylinder containing a liquied at which its turbulance occurs depends on visocisity η density ρ and disntac d between wall of the cylinder. Obtain an expression for ωc using method of dimensios.
View SolutionAssuming that the critical velocity of flow of a liquid through a narrow tube depends on the radius of the tube, density of the liquid and viscosity of the liquid, find an expression for critical velocity.
View Solution
Knowledge Check
Two cylinders having radii 2R and R and moment of inertia 4I and I about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
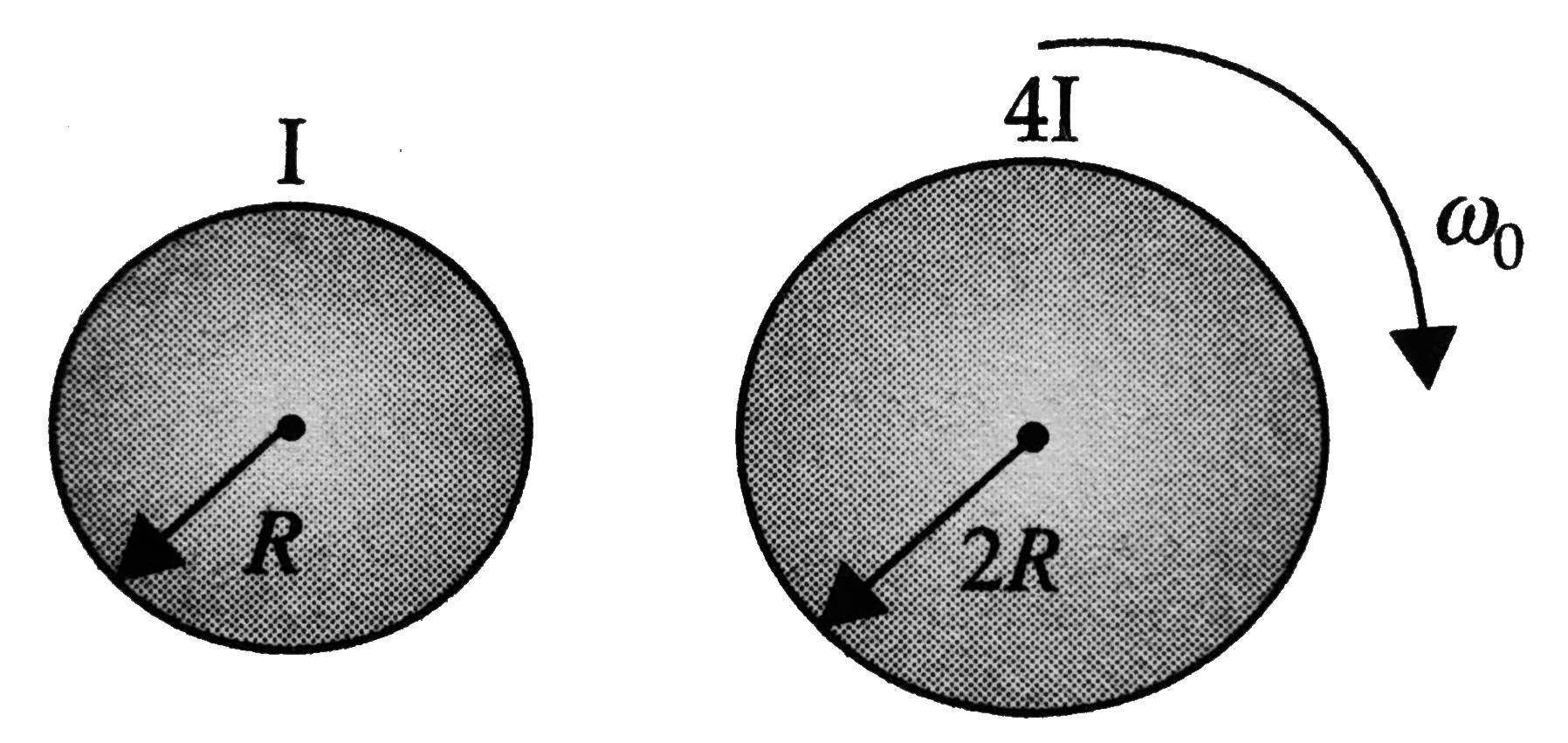 Aangular momentum of system is conservedBkinetic energy is conservedCneither the angular momentum nor the kinetic energy is conservedDboth the angular momentum and kinetic energy are conserved
Aangular momentum of system is conservedBkinetic energy is conservedCneither the angular momentum nor the kinetic energy is conservedDboth the angular momentum and kinetic energy are conservedA cylinder of mass m radius R is spined to a clockwise angular velocity ωo and then gently placed on an inclined plane for which coefficient of friction μ=tanθ,θ is the angle of inclined plane with the horizontal. The centre of mass of cylinder will remain stationary for time
 AωoR/gsinθB2ω)(o)R/3gsinθC2ωoR/5sinθDωoR/2gsinθ
AωoR/gsinθB2ω)(o)R/3gsinθC2ωoR/5sinθDωoR/2gsinθ
Two cylinders having radiii R1 and R2 and rotational inertia I1 and I2 respectively, are supported by fixed axes perpendicular to the plane of figure-5.52. The large cylinder is initially rotating with angular velocityω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually, slipping ceases, and the two cylinders rotate at constant rates in opposite directions, (a) Find the final angular velocity ω2 of the small cylinder in terms of I1,I2,R1,R2 and ω0. (b) Is total angular momentum conserved in this case ?
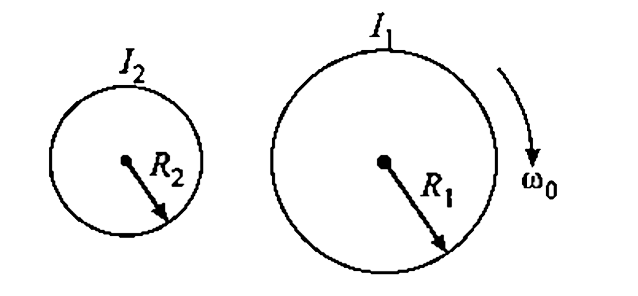
View SolutionA cylinder rests on a horizontal rotating disc, as shown in the figure. Find at what angular velocity, ω, the cylinder falls off the disc, if the distance between the axes of the disc and cylinder is R, and the coefficient of friction μ>D/h where D is the diameter of the cylinder and It is its height.

View SolutionA long cylinder of radius R1 is displaced along its axis with a constant velocity v0 inside a stationary co-axial cylinder of radius R2. The space between the cylinders is filled with viscous liquid. Find the velocity of the liquid as a function of the distance r from the axis of the cylinders. The flow is laminar.
View SolutionFind the mass of a mole of colloid particles if during their centrifuging with an angular velocity ω about a vertical axis the concentration of the particles at the distance r2 from the rotation axis is η times greater than that at the distance r1 (in the same horizontal plane). The densities of the particles and the solvent are equal to ρ and to ρ0 respectively.
View SolutionAn infinite cylinder of radius r with surface charge density σ is rotated about its central axis with angular speed ω. Then the magnetic field at any point inside the cylinder is
View SolutionA gas fills up the space between two long coaxial cylinders of radii R1 and R2, with R1<R2. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. The moment of friction forces acting on a unit length of the inner cylinder is equal to N1. Find the viscosity coefficient η of the gas taking into account that the friction force acting on a unit area of the cylindrical surface of radius r is determined by the formule σ=ηr(∂ω/∂r).
View Solution
