In terms of potential difference V, electric current I, permitivity ε0, permeability μ0 and speed of light c, the dimensionally correct equations (s) is (are) :
μ0I2=ε0V2
ε0I=μ0V
I=ε0cV
μ0cI=ε0V
Step by step video & image solution for In terms of potential difference V, electric current I, permitivity epsi_(0), permeability mu_(0) and speed of light c, the dimensionally correct equations (s) is (are) : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
What is the potential difference VB−VA when the current i is 5A and is decreasing at a rate of 103A /s
View SolutionThe optical properties of a medium are governed by the relative permittivity (εr) and relative permeability (μr). The refractive index is defined as √μrεr=n. For ordinary material, εr>0 and μr>0 and the positive sign is taken for the squre root.
In 1964, a Russian scientist V. Veselago postualted the existance of material with εr<0 and μr<0 . Since, then such metamaterial have been produced in the laboratories and their optical properties studied. For such materials n=−√μrεr. As light enters a medium of such refractive index the phases travel away from the direction of propagation.
(i) According to the description above show that if rays of light enter such a medium from air ( refractive index =1) at an angle theta in 2nd quadrant, then the refracted beam is in the 3rd quadrant.
(ii) Prove that Snell's law holds for such a medium.View Solution
Knowledge Check
- Question 1 - Select One or More
In terms of potential difference C, electric currentI , permittivity ε0, permeability μ0 and speed of light c, the dimensionally correct equation (s) is (are)
A(a) μ0I2=ε0V2B(b) μ0I=μ0VC( c ) I=ε0cVD(d) μ0cI=ε0V - Question 2 - Select One
In terms of potential difference V, electric current I, permittivity ε0 permeability μ0 and speed of light c, the dimensionally correct equation (s) is (are) :
Aμ0I2=ε0V2Bε0I=μ0VCI=ε0cVDBoth A and C - Question 3 - Select One
The curves (a),(b),(c) and (d) show the variation between the applied potential difference (V) and the photoelectric current (i) , at two different intensities of light (I1>I2). In which figure is the correct variation shown ?
A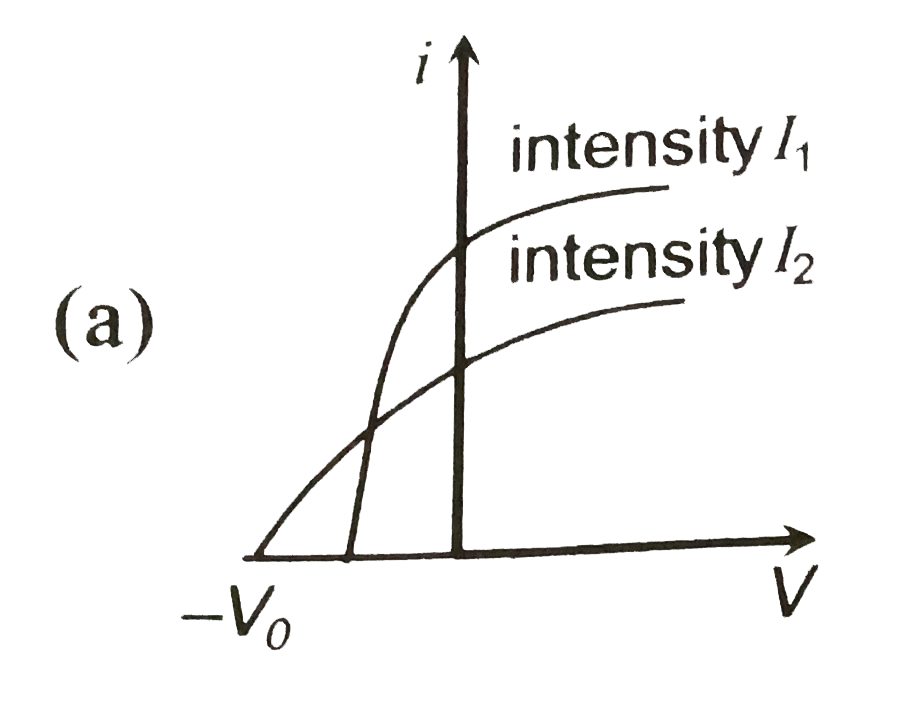 B
B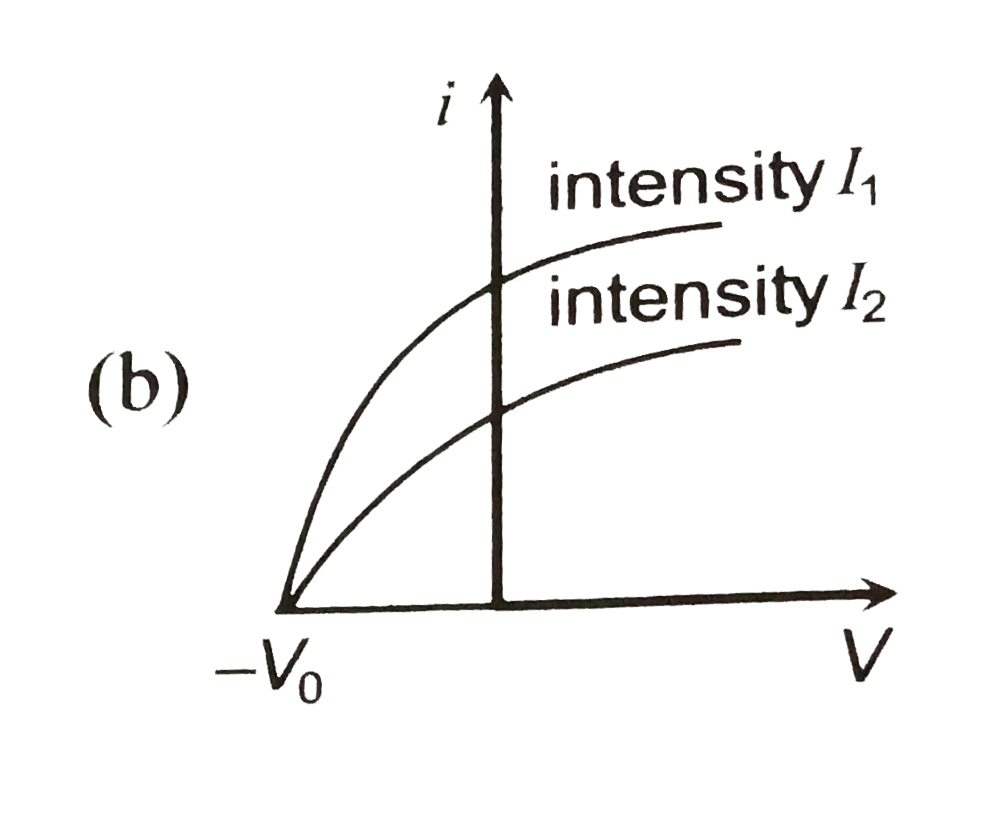 C
C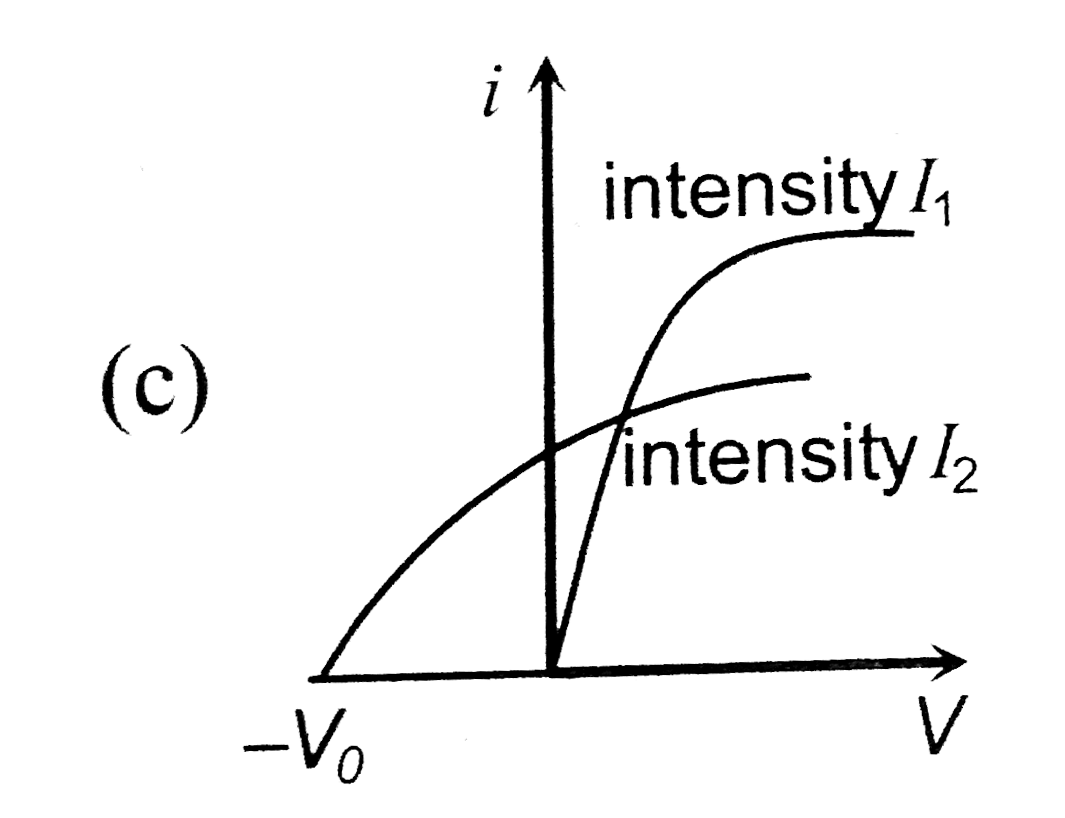 D
D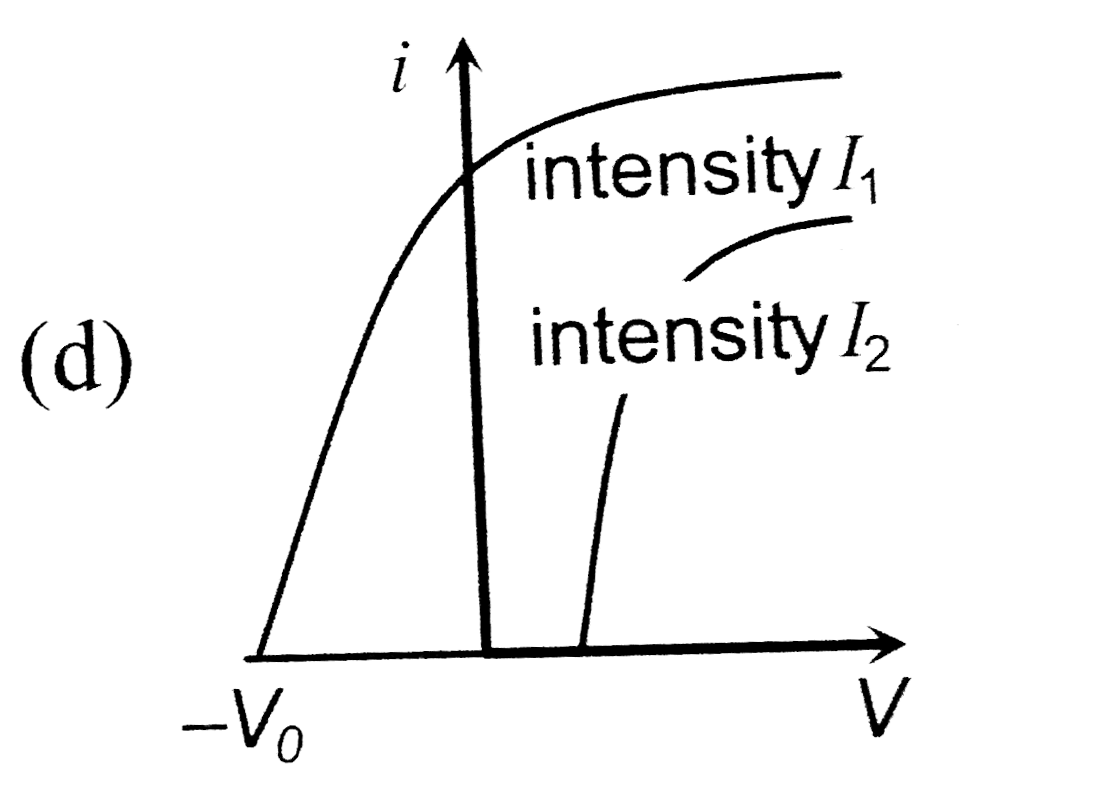
Using method of dimensions, establish the relation among the given quantities.
(a) The potential difference V across a conductor depends on current i flowing in it and resistance of conductor R.
(b) The speed of light c can be expressed in terms of free space μ0.
The energy U stored in an inductor is function of inductance L and current i flowing through it.
(d) The time constant τ to R−C circuit can be expressed in terms of resistance R and capacitance. C.
Dimensional formulae:
V:ML2T−3A−1.R:ML2T−3A−2,
∈0:M−1L−3T4A2,μ0:MLT−2A2,
L:ML2T−2A−2,C:M−1L−2T4A2View SolutionIf 220 V potential difference is applied across an electric bulb, a current of 0.45 A flows in the bulb . What must be the power of the bulb ?
View SolutionStopping potential depends on planks constant (h), current (I), universal gravitational constant (G) and speed of light (C) choose the correct option for the dimension of stopping potential (V).
View SolutionThe optical properties of a medium are governed by the relative permitivity (εr) and relative permeability (μr). The refractive index is defined as √μ1εr=n . For ordinary sing is taken for the square root. In 1964, a Russian scientist V. Veselago postulated the existence of material with εr<0 and μr<0 . Since then such 'meta materials' have been produced in the laboratorised and their optical properties studied. For such materials n=−√μrεr. As light entes a medium of such refractive index the phases traval away front the direction ofpropagation.
Consider following statements
i) Snall's slaw valid for these mater ials
ii) Snell's slaw is not valid for these mater ials
iii) Speed of light in these mater ial is v=c|n|
iv) Speed of light in these material is v=cView SolutionIn an electric circuit, potential difference across a lamp is 20 V and current through the lamp is 0.5A. The resistance of the lamp is
View Solution

