A ball rolls down an inclined trck 2 m long in 4s. Find speed of the ball at the bottom of the track.
To find the speed of the ball at the bottom of the inclined track, we can use the equations of motion. Here are the steps to solve the problem:
Step 1: Identify the given values
- Distance (s) = 2 meters
- Time (t) = 4 seconds
- Initial velocity (u) = 0 m/s (since the ball starts from rest)
Step 2: Use the equation of motion
We can use the equation of motion:
s=ut+12at2
Substituting the known values into the equation:
2=0⋅4+12a(42)
This simplifies to:
2=12a(16)
2=8a
Step 3: Solve for acceleration (a)
To find the acceleration, we rearrange the equation:
a=28=14 m/s2
Step 4: Use the acceleration to find final velocity (v)
Now, we can use another equation of motion to find the final velocity:
v=u+at
Substituting the known values:
v=0+(14)(4)
v=1 m/s
Conclusion
The speed of the ball at the bottom of the track is 1 m/s.
---
- Distance (s) = 2 meters
- Time (t) = 4 seconds
- Initial velocity (u) = 0 m/s (since the ball starts from rest)
We can use the equation of motion:
s=ut+12at2
Substituting the known values into the equation:
2=0⋅4+12a(42)
This simplifies to:
2=12a(16)
2=8a
To find the acceleration, we rearrange the equation:
a=28=14 m/s2
Now, we can use another equation of motion to find the final velocity:
v=u+at
Substituting the known values:
v=0+(14)(4)
v=1 m/s
The speed of the ball at the bottom of the track is 1 m/s.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A ball rolls down an inclined plane and acquires a velocity vr when it reaches the bottom of the plane. If the same ball slides without friction and acquires rolling from the same height down an equally inclined smooth plane and acquires a velocity vs (then which of the following statements are not correct?
Avr<vs because a work is done by the rolling ball against the frictional force.Bvr>vs, because the angular velocity acquired makes the rolling ball to travel fasterCvr=vs because kinetic energy of the two balls is same at the bottom of the planes.Dvr>vs because the rolling ball acquires rotational as well as translational kinetic energy.A hollow sphere rolls down a 30∘ incline of length 6m without slipping. The speed of centre of mass at the bottom of plane is
A6ms−1B3ms−1C6√2ms−1D3√3ms−1A solid cylinder rolls down an inclined plane of height 3m and reaches the bottom of plane with angular velocity of 2√2rad/s. The radius of cylinder must be [take g=10m/s2]
A5cmB0.5cmC√10cmD√5m
A ball rolls down an inclined track 2 m long 4s. Find (i) acceleration (ii) time taken to cover the second metre of the track and (iii) speed of the vall at the bottom of the track.
View SolutionA uniform ring rolls down an inclined plane without slipping. If it reaches the bottom of a speed of 2m/s, then calculate the height of the inclined plane (use g=10m/s2)
View SolutionA sphere rolls up an inclined plane whose inclination is 30∘. At the bottom of the inclined plane, the center of mass of the sphere has a translational speed of 5ms−1 (a) How far does the sphere travel up the plane? (b) How long does it take to return to the bottom?
View SolutionA ball rolls down an inclined plane, figure. The ball is first released from rest from P and then later from Q.
Which of the following statement is//are correct ?
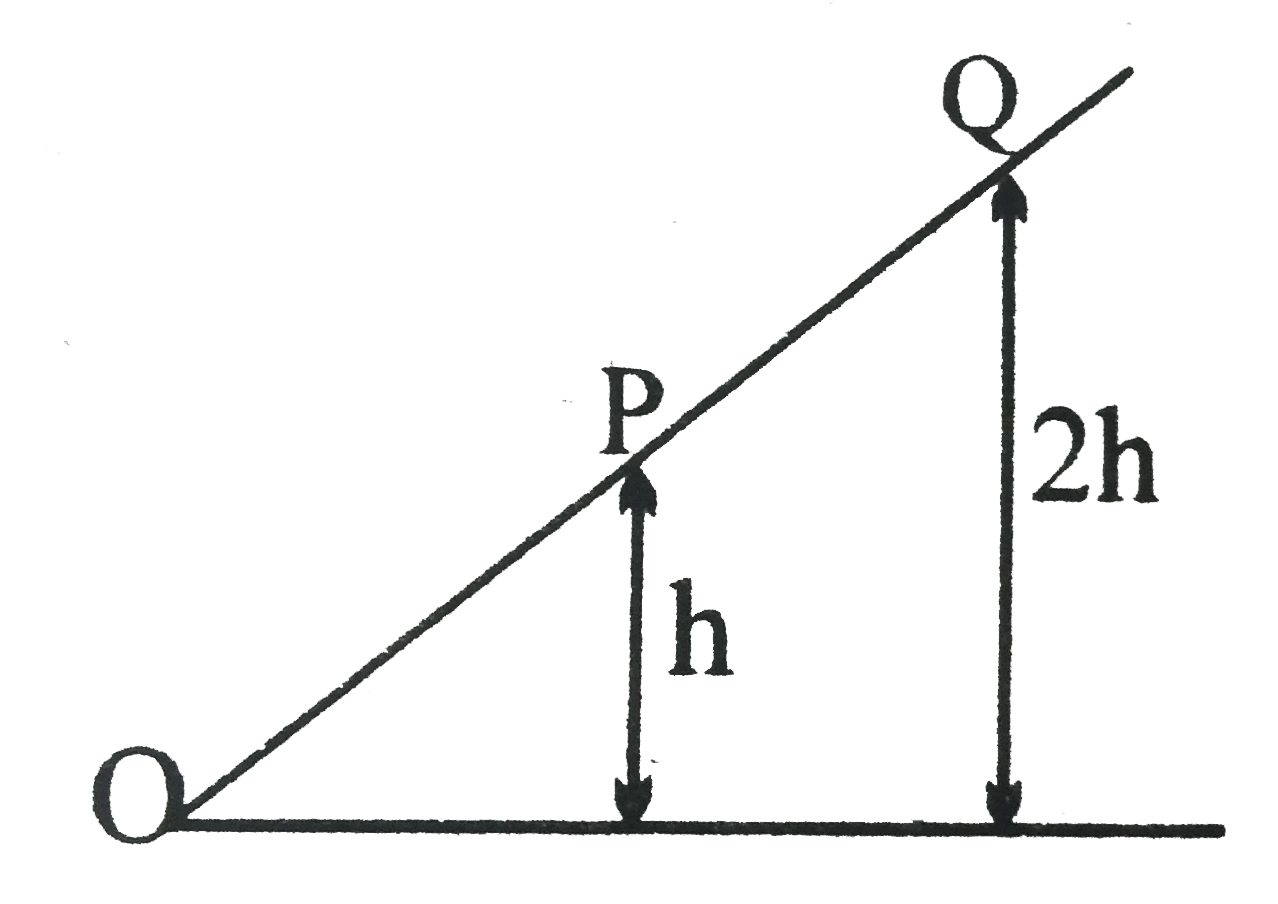 .
.
(i) The ball takes twice as much time to roll from Q to O as it does to roll from P to O.
(ii) The acceleration of the ball at Q is twice as large as the acceleration at P.
(iii) The ball has twice as much K.E at O when rolling from Q as it does when rolling from P.
View SolutionA solid cylinder 30 cm in diameter at the top of an inclined plane 2.0 m high is released and rolls down the incline without loss of energy due to friction. Its linear speed at the bottom is
View Solution
