A solid cylinder 30 cm in diameter at the top of an inclined plane 2.0 m high is released and rolls down the incline without loss of energy due to friction. Its linear speed at the bottom is
5.29 m/sec
41 m/sec
51 m/sec
51 cm/sec
The correct Answer is:A
To solve the problem of finding the linear speed of a solid cylinder rolling down an inclined plane, we can use the principle of conservation of mechanical energy. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the given information
- Diameter of the cylinder = 30 cm, hence radius r=302=15 cm = 0.15 m
- Height of the inclined plane h=2.0 m
- Initial velocity u=0 (the cylinder is released from rest)
Step 2: Write the conservation of mechanical energy equation
According to the conservation of mechanical energy, the total mechanical energy at the top of the incline (potential energy) equals the total mechanical energy at the bottom (kinetic energy).
At the top:
- Potential Energy (PE) = mgh
- Kinetic Energy (KE) = 0 (since it is at rest)
At the bottom:
- Potential Energy (PE) = 0 (since it is at the reference level)
- Kinetic Energy (KE) = Translational KE + Rotational KE
- Translational KE = 12mv2
- Rotational KE = 12Iω2
Step 3: Determine the moment of inertia and relate linear and angular velocity
For a solid cylinder, the moment of inertia I about its center of mass is given by:
I=12mr2
Using the rolling condition, the relationship between linear speed v and angular speed ω is:
v=rω
Thus,
ω=vr
Step 4: Substitute into the kinetic energy equation
Substituting ω into the rotational kinetic energy:
KE=12mv2+12(12mr2)(vr)2
KE=12mv2+14mv2
KE=34mv2
Step 5: Set up the energy conservation equation
Setting the total mechanical energy at the top equal to that at the bottom:
mgh=34mv2
Step 6: Cancel mass and solve for v2
Cancel m from both sides:
gh=34v2
Rearranging gives:
v2=4gh3
Step 7: Substitute the values of g and h
Using g=9.8m/s2 and h=2.0m:
v2=4×9.8×23
v2=78.43
v2=26.1333
Step 8: Calculate v
Taking the square root:
v=√26.1333≈5.11m/s
Final Answer:
The linear speed of the solid cylinder at the bottom of the incline is approximately 5.11 m/s.
---
- Diameter of the cylinder = 30 cm, hence radius r=302=15 cm = 0.15 m
- Height of the inclined plane h=2.0 m
- Initial velocity u=0 (the cylinder is released from rest)
According to the conservation of mechanical energy, the total mechanical energy at the top of the incline (potential energy) equals the total mechanical energy at the bottom (kinetic energy).
- Potential Energy (PE) = mgh
- Kinetic Energy (KE) = 0 (since it is at rest)
- Potential Energy (PE) = 0 (since it is at the reference level)
- Kinetic Energy (KE) = Translational KE + Rotational KE
- Translational KE = 12mv2
- Rotational KE = 12Iω2
For a solid cylinder, the moment of inertia I about its center of mass is given by:
I=12mr2
v=rω
Thus,
ω=vr
Substituting ω into the rotational kinetic energy:
KE=12mv2+12(12mr2)(vr)2
KE=12mv2+14mv2
KE=34mv2
Setting the total mechanical energy at the top equal to that at the bottom:
mgh=34mv2
Cancel m from both sides:
gh=34v2
Rearranging gives:
v2=4gh3
Using g=9.8m/s2 and h=2.0m:
v2=4×9.8×23
v2=78.43
v2=26.1333
Taking the square root:
v=√26.1333≈5.11m/s
The linear speed of the solid cylinder at the bottom of the incline is approximately 5.11 m/s.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)
10 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on kinetic energy, work and power)
30 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
A solid cylinder at rest at top of an inclined plane of height 2.7 m rolls down without slipping. If the same cylinder has to slide down a frictionless inclined plane and acquires the same velocity as that acquired by centre of mass of rolling cylinder at the bottom of the incline, what should be the height of inclined plane?
View SolutionA solid cylinder at rest at top of an inclined plane of height 2.7m rolls down without slipping. If the same cylinder has to slide down a frictionaly inclined plane and acquires the same velocity as that acquired by centre of mass of rolling cylinder at the bottom of the incline, what should be the height of inclined plane ?
View Solution
Knowledge Check
A solid sphere at the top of an inclined plane 0.6 m high is released and rolls down the incline without slipping and without loss of energy due to friction. Its linear speed at the bottom is about
A2.9m/sB2.42m/sC3.87m/sD1.53m/sA solid cylinder is rolling without slipping down an inclined plane. Then its angular momentum is :
AConserved about COM of the cylinderBConserved about point of contactCConserved about all the pointsDNot conserved about any pointA solid cylinder is rolling down a rough inclined plane of inclination θ. Then
AThe friction force is dissipativeBThe friction force is necessarily changingCThe friction force will aid rotation but hinder translationDThe friction force is reduced if θ is reduced
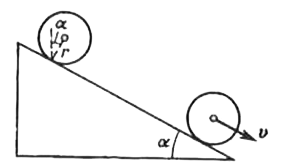
A solid cylinder with base radius jis placed on top of an inclined plane of length land slope angle α (Fig). The cylinder rolls down without slipping. Find the speed of the centre of mass of the cylinder at the bottom of the plane, if the coefficient of rolling friction is k. Can rolling friction be neglected? Do the calculation for the following conditions: l=1m,α=30∘,r=10cm,k=5×10−4m . What would be the speed if, in the absence of friction, the cylinder slides down?
View SolutionA cylinder is released from rest from the top of an incline of inclination θ and length. If the cylinder rolls without slipping. What will be its speed whenit reaches the bottom?
View SolutionA cylinder is released from rest from the top of an incline of inclination θ and length l. If the cylinder roles without slipping, its speed at the bottom
View SolutionA solid cylinder rolls down from an inclined plane of height h. What is the velocity of the cylinder when it reaches at the bottom of the plane ?
View SolutionA solid sphere rolls down without slipping from rest on a 30∘ incline. Its linear acceleration is
View Solution
