Draw the following graphs (expected nature only) between distance and time of an object in case of:For a body moving with uniform velocity.
To draw the graph between distance (s) and time (t) for a body moving with uniform velocity, we can follow these steps:
1. Understand the Concept of Uniform Velocity:
- Uniform velocity means that the object covers equal distances in equal intervals of time. There is no change in speed, and hence, the acceleration is zero.
2. Identify the Relationship:
- The relationship between distance and time for uniform velocity can be expressed with the equation:
s=ut
- Here, s is the distance, u is the uniform velocity, and t is the time.
3. Graph Characteristics:
- Since the equation s=ut is linear, the graph will be a straight line.
- The slope of the line represents the uniform velocity u.
4. Plotting the Graph:
- On the x-axis, plot time t.
- On the y-axis, plot distance s.
- Start from the origin (0,0) because at time t=0, the distance s is also 0.
5. Drawing the Line:
- Draw a straight line from the origin that extends upwards to the right. The angle of the line with the x-axis will depend on the value of the uniform velocity u.
- The steeper the line, the greater the velocity.
6. Labeling the Graph:
- Label the axes: x-axis as "Time (t)" and y-axis as "Distance (s)".
- Optionally, indicate the slope as u (the uniform velocity).
Final Graph:
The resulting graph will be a straight line starting from the origin (0,0) and extending in the first quadrant, indicating that as time increases, distance also increases linearly.
---
- Uniform velocity means that the object covers equal distances in equal intervals of time. There is no change in speed, and hence, the acceleration is zero.
- The relationship between distance and time for uniform velocity can be expressed with the equation:
s=ut
- Here, s is the distance, u is the uniform velocity, and t is the time.
- Since the equation s=ut is linear, the graph will be a straight line.
- The slope of the line represents the uniform velocity u.
- On the x-axis, plot time t.
- On the y-axis, plot distance s.
- Start from the origin (0,0) because at time t=0, the distance s is also 0.
- Draw a straight line from the origin that extends upwards to the right. The angle of the line with the x-axis will depend on the value of the uniform velocity u.
- The steeper the line, the greater the velocity.
- Label the axes: x-axis as "Time (t)" and y-axis as "Distance (s)".
- Optionally, indicate the slope as u (the uniform velocity).
The resulting graph will be a straight line starting from the origin (0,0) and extending in the first quadrant, indicating that as time increases, distance also increases linearly.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The graph between displacement and time for a particle moving with uniform acceleration is a
Astraight line with a positive slopeBparabolaCellipseDstraight line parallel to time axis - Question 2 - Select One
The slope of a distance-time graph of a moving object indicates :
Adistance moved by the objectBtime taken by the objectCspeed of the objectDposition of the object - Question 3 - Select One
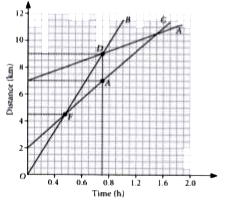
Given figure shows the distance - time graph of three object A, B and C as time is taken on x- axis and distance is taken on y - axis . The slope of the distance - time graph of an object represents its speed .
The magnitude of displacement equal to the distance travelled by the object , then we can use the term uniform velocity in place of uniform speed
Choose the correct distance - time graph for an object moving with uniform velocityA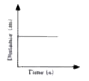 B
B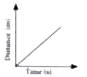 C
C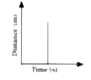 D
D
Draw distance time graph of a body moving with constant acceleration.
View SolutionDraw the velocity-time graph of an object moving with uniform positive acceleration.
View SolutionDraw the velocity-time graph of an object moving with uniform negative acceleration.
View SolutionWhat is the nature of the distance time graph for an object moving uniformly along a straight long road ?
View SolutionDraw velocity time graph of a body moving with constant retardation.
View Solution

