TRUE/FALSE TYPE QUESTIONS: A pilot looping a vertical loop does notfall down even at the highest point.
To determine whether the statement "A pilot looping a vertical loop does not fall down even at the highest point" is true or false, we can analyze the forces acting on the pilot at the highest point of the loop.
1. Understanding the Scenario:
- The pilot is in a plane that is looping vertically. At the highest point of the loop, the plane is upside down.
2. Forces Acting on the Pilot:
- At the highest point of the loop, two main forces act on the pilot:
- The gravitational force (weight) acting downward, which is mg (where m is the mass of the pilot and g is the acceleration due to gravity).
- The centripetal force required to keep the pilot moving in a circular path, which is provided by the plane's velocity. This force can be expressed as mv2r (where v is the velocity of the plane and r is the radius of the loop).
3. Condition for the Pilot to Stay in the Plane:
- For the pilot not to fall, the centripetal force must be sufficient to counteract the gravitational force. This means that:
mv2r≥mg
- Rearranging this inequality gives:
v2≥rg
- This condition implies that the velocity of the plane at the highest point must be high enough to ensure that the required centripetal force is at least equal to the gravitational force.
4. Conclusion:
- If the velocity v is sufficient to satisfy the condition v2≥rg, then the pilot will not fall down at the highest point of the loop. Therefore, the statement is TRUE.
Final Answer:
The statement "A pilot looping a vertical loop does not fall down even at the highest point" is TRUE.
- The pilot is in a plane that is looping vertically. At the highest point of the loop, the plane is upside down.
- At the highest point of the loop, two main forces act on the pilot:
- The gravitational force (weight) acting downward, which is mg (where m is the mass of the pilot and g is the acceleration due to gravity).
- The centripetal force required to keep the pilot moving in a circular path, which is provided by the plane's velocity. This force can be expressed as mv2r (where v is the velocity of the plane and r is the radius of the loop).
- For the pilot not to fall, the centripetal force must be sufficient to counteract the gravitational force. This means that:
mv2r≥mg
- Rearranging this inequality gives:
v2≥rg
- This condition implies that the velocity of the plane at the highest point must be high enough to ensure that the required centripetal force is at least equal to the gravitational force.
- If the velocity v is sufficient to satisfy the condition v2≥rg, then the pilot will not fall down at the highest point of the loop. Therefore, the statement is TRUE.
The statement "A pilot looping a vertical loop does not fall down even at the highest point" is TRUE.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Figure shows a loop model (loop L) for a diamagnetic material.
 Athe net dipole moment of the loop directed to wards the magnetBThe net dipole moment of the loop directed away from the loopCThe loop gets attracted towards the magnetDThe loop gets repelled by the magnet
Athe net dipole moment of the loop directed to wards the magnetBThe net dipole moment of the loop directed away from the loopCThe loop gets attracted towards the magnetDThe loop gets repelled by the magnetFigure shows a loop model (loop L) for a diamgnetic material.
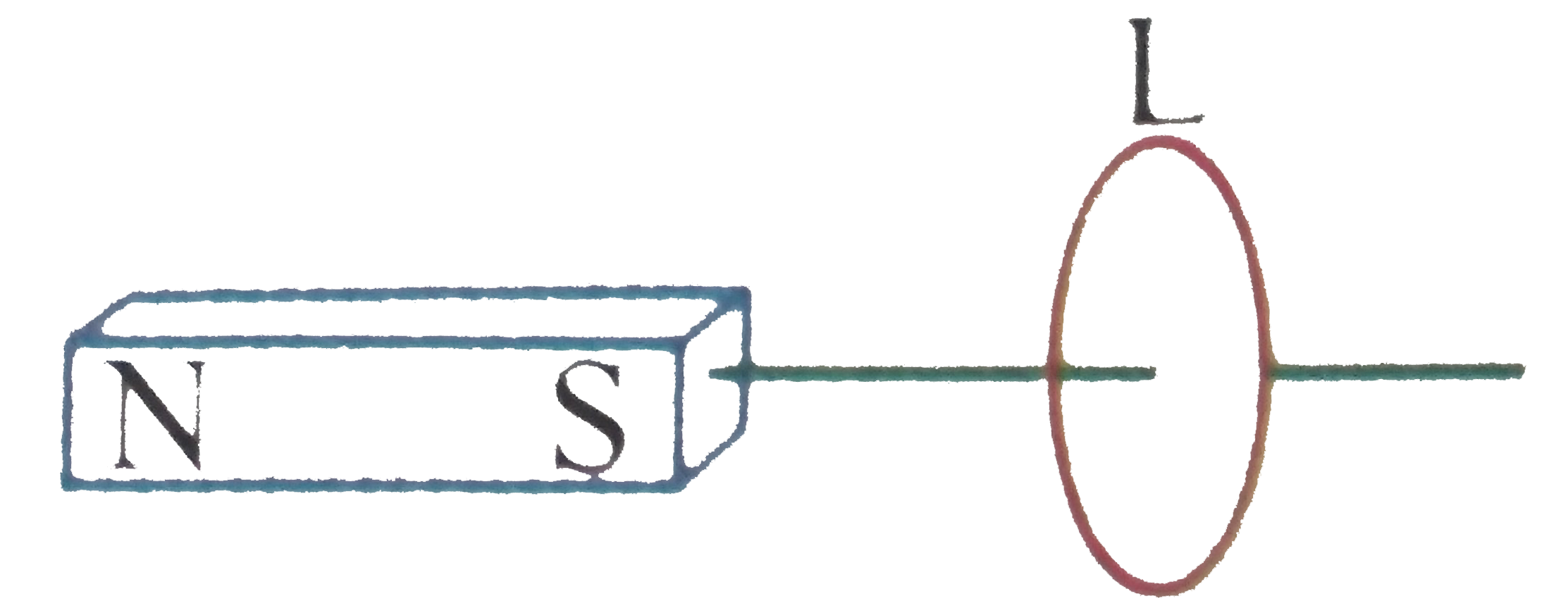 Athe net dipole moment of the loop directed towards the magnetBThe net dipole moment of the loop directed away from the loopCThe loop gets attracted towards the magnetDThe loop gets repelled by the magnet
Athe net dipole moment of the loop directed towards the magnetBThe net dipole moment of the loop directed away from the loopCThe loop gets attracted towards the magnetDThe loop gets repelled by the magnet
Looping and somersaulting types of locomotion are seen in
View SolutionLoop Tracing
View SolutionLoop tracing
View SolutionLoop Tracing
View SolutionTRUE/FALSE TYPE QUESTIONS: A body in linear motion can be in equilibrium
View SolutionWhy does a pilot not fall down when his aeroplane loops a vertical loop ?
View Solution
