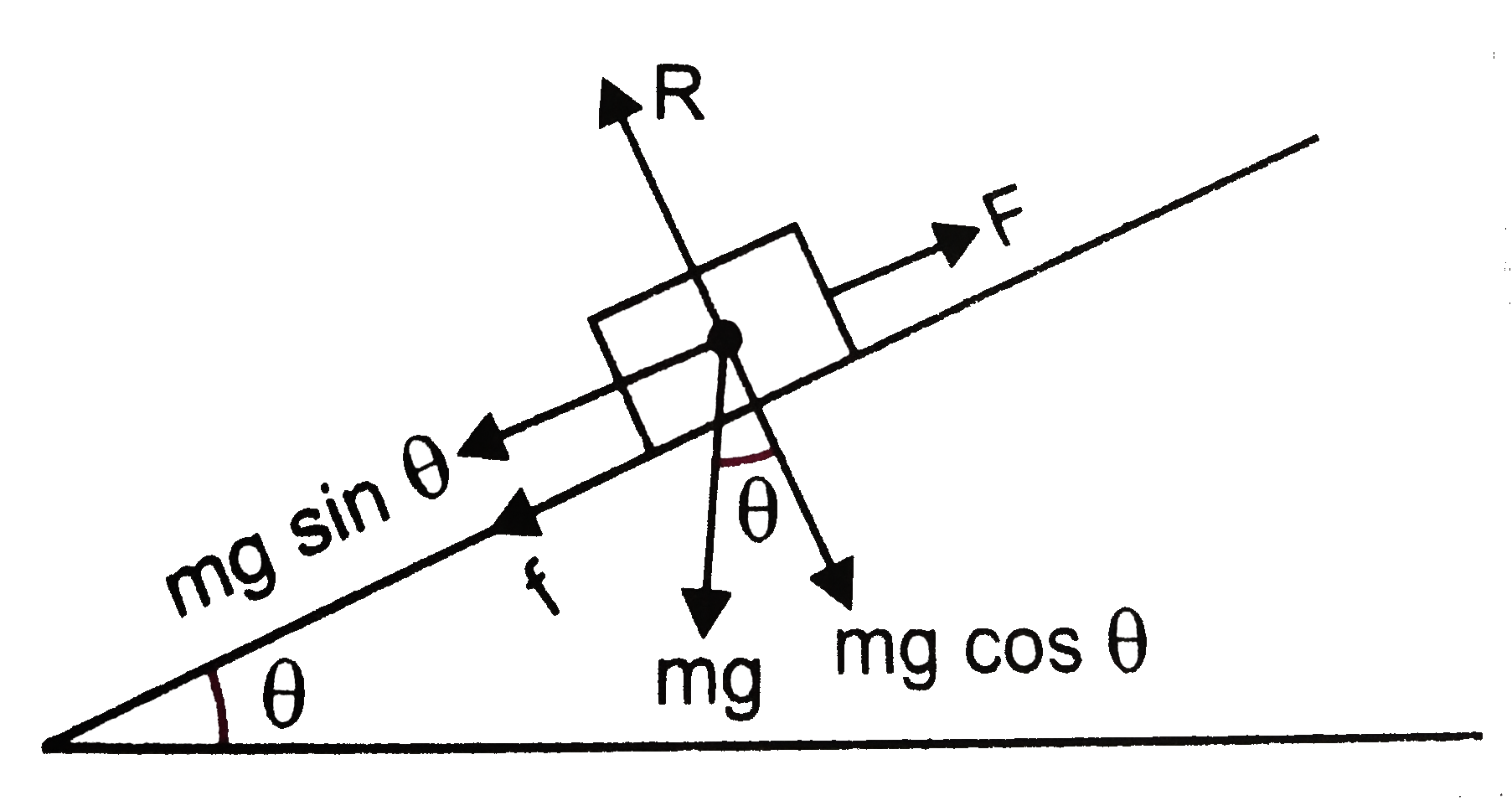
Define the term coefficient of limiting friction between the surfaces. A body of mass 10 kg is placed on an inclined surface of angle 30∘. If the coefficient of limiting friction is 1/√3 , find the force required to just push the body up the inclined plane. The force is being applied parallel to the inclined surface.
To solve the problem step by step, we will first define the coefficient of limiting friction and then calculate the force required to push the body up the inclined plane.
Step 1: Define the Coefficient of Limiting Friction
The coefficient of limiting friction (μ) is defined as the ratio of the maximum static frictional force (F_s_max) that can act between two surfaces before they start to slide over each other to the normal force (N) acting between those surfaces. Mathematically, it can be expressed as:
μ=FsmaxN
Step 2: Identify Given Data
- Mass of the body (m) = 10 kg
- Angle of inclination (θ) = 30°
- Coefficient of limiting friction (μ) = 1√3
- Acceleration due to gravity (g) = 10 m/s² (approximate value)
Step 3: Calculate the Forces Acting on the Body
1. Weight of the body (W):
W=m⋅g=10kg⋅10m/s2=100N
2. Components of the weight:
- Perpendicular to the incline:
W_{\perpendicular} = W \cdot \cos(\theta) = 100 \cdot \cos(30°) = 100 \cdot \frac{\sqrt{3}}{2} = 50\sqrt{3} \, \text{N}
- Parallel to the incline:
W∥=W⋅sin(θ)=100⋅sin(30°)=100⋅12=50N
Step 4: Calculate the Normal Force (N)
The normal force (N) acting on the body is equal to the perpendicular component of the weight:
N = W_{\perpendicular} = 50\sqrt{3} \, \text{N}
Step 5: Calculate the Maximum Static Frictional Force (F_s_max)
Using the coefficient of limiting friction:
Fsmax=μ⋅N=1√3⋅50√3=50N
Step 6: Calculate the Total Force Required to Push the Body Up
To just push the body up the incline, the applied force (F) must overcome both the component of weight acting down the incline and the maximum static frictional force:
F=W∥+Fsmax=50N+50N=100N
Final Answer
The force required to just push the body up the inclined plane is:
100N
The coefficient of limiting friction (μ) is defined as the ratio of the maximum static frictional force (F_s_max) that can act between two surfaces before they start to slide over each other to the normal force (N) acting between those surfaces. Mathematically, it can be expressed as:
μ=FsmaxN
- Mass of the body (m) = 10 kg
- Angle of inclination (θ) = 30°
- Coefficient of limiting friction (μ) = 1√3
- Acceleration due to gravity (g) = 10 m/s² (approximate value)
1. Weight of the body (W):
W=m⋅g=10kg⋅10m/s2=100N
- Perpendicular to the incline:
W_{\perpendicular} = W \cdot \cos(\theta) = 100 \cdot \cos(30°) = 100 \cdot \frac{\sqrt{3}}{2} = 50\sqrt{3} \, \text{N}
- Parallel to the incline:
W∥=W⋅sin(θ)=100⋅sin(30°)=100⋅12=50N
The normal force (N) acting on the body is equal to the perpendicular component of the weight:
N = W_{\perpendicular} = 50\sqrt{3} \, \text{N}
Using the coefficient of limiting friction:
Fsmax=μ⋅N=1√3⋅50√3=50N
To just push the body up the incline, the applied force (F) must overcome both the component of weight acting down the incline and the maximum static frictional force:
F=W∥+Fsmax=50N+50N=100N
The force required to just push the body up the inclined plane is:
100N
Topper's Solved these Questions
Similar Questions
A body of mass 10 kg is placed on an inclined surface of angle 30∘ . If coefficient of limiting friction is 1/√3 , find the inclined plane. Force is being exerted parallel to the inclined plane
 .
.
View SolutionA mass of 200 kg is placed on a rough inclined plane of angle 30∘ . If coefficient of limiting friction is 1/√3 , find the least forces in newton , acting parallel to the plane (i) to keep the mass from sliding down (ii) to move the mass up the plane.
View Solution
Knowledge Check
A body of mass 10 kg is lying on a rough plane inclined at an angle of 30∘ to the horizontal and the coefficient of friction is 0.5. the minimum force required to pull the body up the plane is
A914 NB91.4 NC9.14 ND0.914 NA block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
Amgsinθ+μmgcosθBmgcosθ−μmgsinθCmgsinθ−μmgcosθDmgcosθ+μmgsinθA body is sliding down an inclined plane forming an angle 30∘ with the horizontal. If the coefficient of friction is 0.3 then acceleration of the body is
A1.25ms−2B2.35ms−2C3.4ms−2D4.9ms−2
A mass of 100kg is resting on a rough inclined plane of angle 30∘ If the coefficient of friction is 1/√3 find the greatest and the least forces that acting parallel to the plane in both cases just maintain the mass in equilibrium .
View SolutionA block is moving on an inclined plane making an angle 45∘ with the horizontal and the coefficient of friction is μ. The force required to just push it up the inclined plane is 3 times the force required to just prevent it from sliding down. If we define N=10μ, then N is
View SolutionA body is sliding down an inclined plane forming an angle 30∘ with the horizantal. If the coefficient of friction is0.3 then acceleration of the body is
View SolutionA block of mass 5 kg slides down a rough inclined surface. The angle of inclination is 45∘. The coefficient of sliding friction is 0.20. When the block slides 10 cm, the work done on the block by force of friction is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View Solution