Two bodies A and B having mass m and M respectively ppossess same kinetic energy. Given that M>m. If pA and pB be their moments, then which of the following statements is true?
pA=pB
) pA>pB
) pA<pB
It cannot be predicted
To solve the problem, we need to analyze the kinetic energies and momenta of the two bodies A and B, given that they have the same kinetic energy but different masses.
1. Understanding Kinetic Energy:
The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
For body A with mass m and velocity v1, the kinetic energy is:
KEA=12mv21
For body B with mass M and velocity v2, the kinetic energy is:
KEB=12Mv22
2. Setting Kinetic Energies Equal:
Since both bodies have the same kinetic energy:
12mv21=12Mv22
We can simplify this equation by canceling 12:
mv21=Mv22
3. Finding the Relationship Between Velocities:
Rearranging the equation gives:
v21v22=Mm
Taking the square root of both sides, we find:
v1v2=√Mm
This implies:
v1=v2√Mm
4. Calculating Momentum:
The momentum p of an object is given by:
p=mv
Thus, the momentum of body A is:
pA=mv1=m(v2√Mm)=v2√mM
The momentum of body B is:
pB=Mv2
5. Comparing Momentums:
Now we compare pA and pB:
pA=v2√mMandpB=Mv2
Dividing both momenta by v2 (assuming v2≠0):
pApB=√mMM=√mM
Since M>m, it follows that √mM<1. Therefore:
pA<pB
Conclusion:
The momentum of body A is less than the momentum of body B, i.e., pA<pB.
The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
For body A with mass m and velocity v1, the kinetic energy is:
KEA=12mv21
For body B with mass M and velocity v2, the kinetic energy is:
KEB=12Mv22
Since both bodies have the same kinetic energy:
12mv21=12Mv22
We can simplify this equation by canceling 12:
mv21=Mv22
Rearranging the equation gives:
v21v22=Mm
Taking the square root of both sides, we find:
v1v2=√Mm
This implies:
v1=v2√Mm
The momentum p of an object is given by:
p=mv
Thus, the momentum of body A is:
pA=mv1=m(v2√Mm)=v2√mM
The momentum of body B is:
pB=Mv2
Now we compare pA and pB:
pA=v2√mMandpB=Mv2
Dividing both momenta by v2 (assuming v2≠0):
pApB=√mMM=√mM
Since M>m, it follows that √mM<1. Therefore:
pA<pB
The momentum of body A is less than the momentum of body B, i.e., pA<pB.
Topper's Solved these Questions
Similar Questions
Two bodies of masses m1 and m2 have equal KE. Their momenta is in the ratio
View SolutionTwo bodies A and B having masses M and 3M respectively are kept at a distance 2.73 m apart. A small particle of mass m is to be place so that the net gravitational force on it, due to A and B is zero. What will be its distance from body A ?
View Solution
Knowledge Check
- Question 1 - Select One
If K, p and m represent the kinetic energy, momentum and mass of a body respectively, then which of the following graphs is incorrect?
A B
B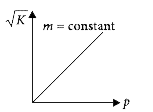 C
C D
D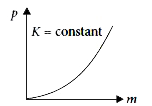
- Question 2 - Select One
A proton (mass m and charge +e) and an α-particle (mass 4 m and charge +2e) are projected with the same kinetic energy at right angles to the uniform magnetic field. Which one of the following statements will be true?
AThe alpha-particle will be bent in a circular path with a small radius that for the protonBThe radius of the path of the alpha-particle will be greater than that of the protonCThe alpha-particle and the proton will be bent in a circular path with the same radiusDThe alpha-particle and the proton will go through the field in a staight line - Question 3 - Select One
Two bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
Am1:m2Bm2:m1C√m1:√m2Dm21:m22
Let P(n) be the statement n3+nis 3m such that m is a positive integer, then which of the following is true?
View SolutionTwo bodies of masses m1andm2 have equal kinetic energies. If P1 and P2 are their respective momentum, then ratio P1:P2 is equal to
View SolutionTwo bodies of masses m1andm2 have equal kinetic energies. If P1andP2 are their respective momentum, then ratio P1:P2 is equal to
View SolutionTwo blocks A and B have masses m and 4m, respectively. Each one is acted upon by a force F. If they acquire the same kinetic energy in time tA and tB, then (tA)/(tB) is
View SolutionM, A and P are the mid-points of the sides DE, DF and EF of Δ DEF respectively. Which of the following statements is true ?
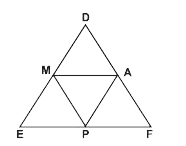 View Solution
View Solution

