Write an expression for the position vector of the centre of mass of n-particle system. Also write the equations of motion which govern the motion of the centre of mass
To derive the expression for the position vector of the center of mass of an n-particle system and the equations of motion governing it, we will follow these steps:
Step 1: Define the System
Consider a system of n particles, where each particle has a mass mi and a position vector →ri given by its coordinates (xi,yi,zi).
Step 2: Position Vector of Center of Mass
The position vector of the center of mass →Rcm of the system can be expressed as the weighted average of the position vectors of all particles. The formula for the position vector of the center of mass is:
→Rcm=1Mn∑i=1mi→ri
where M is the total mass of the system, given by:
M=n∑i=1mi
Step 3: Break Down the Position Vector
The position vector →ri can be expressed in terms of its components:
→ri=(xi,yi,zi)
Thus, the components of the center of mass can be expressed as:
1. X-component:
Xcm=1Mn∑i=1mixi
2. Y-component:
Ycm=1Mn∑i=1miyi
3. Z-component:
Zcm=1Mn∑i=1mizi
Step 4: Equations of Motion for Center of Mass
To find the equations of motion for the center of mass, we differentiate the position vector with respect to time to find the velocity:
→Vcm=d→Rcmdt=1Mn∑i=1mid→ridt=1Mn∑i=1mi→vi
where →vi is the velocity of the i-th particle.
Similarly, differentiating again gives us the acceleration of the center of mass:
→Acm=d→Vcmdt=1Mn∑i=1mid→vidt=1Mn∑i=1mi→ai
where →ai is the acceleration of the i-th particle.
Summary of the Results
1. The position vector of the center of mass is given by:
→Rcm=1Mn∑i=1mi→ri
2. The equations of motion governing the center of mass are:
- Velocity:
→Vcm=1Mn∑i=1mi→vi
- Acceleration:
→Acm=1Mn∑i=1mi→ai
Consider a system of n particles, where each particle has a mass mi and a position vector →ri given by its coordinates (xi,yi,zi).
The position vector of the center of mass →Rcm of the system can be expressed as the weighted average of the position vectors of all particles. The formula for the position vector of the center of mass is:
The position vector →ri can be expressed in terms of its components:
Xcm=1Mn∑i=1mixi
Ycm=1Mn∑i=1miyi
Zcm=1Mn∑i=1mizi
To find the equations of motion for the center of mass, we differentiate the position vector with respect to time to find the velocity:
1. The position vector of the center of mass is given by:
→Rcm=1Mn∑i=1mi→ri
- Velocity:
→Vcm=1Mn∑i=1mi→vi
- Acceleration:
→Acm=1Mn∑i=1mi→ai
Topper's Solved these Questions
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
Similar Questions
Knowledge Check
The centre of mass of two particles system lies
Aat the midpoint on the line joining the two particles.Bat one end of line joining the two particlesCon the line perpendicular to the line joining two particlesDon the line joining the two particlesThe motion of the centre of mass is the result of
AAttractive forcesBRepulsive forcesCExternal forcesDInternal forces
Write an expression for the velocity of the centre of mass of a system of particles.
View SolutionFind out the position of centre of mass of two particle system.
View SolutionPosition of the centre of mass is :-
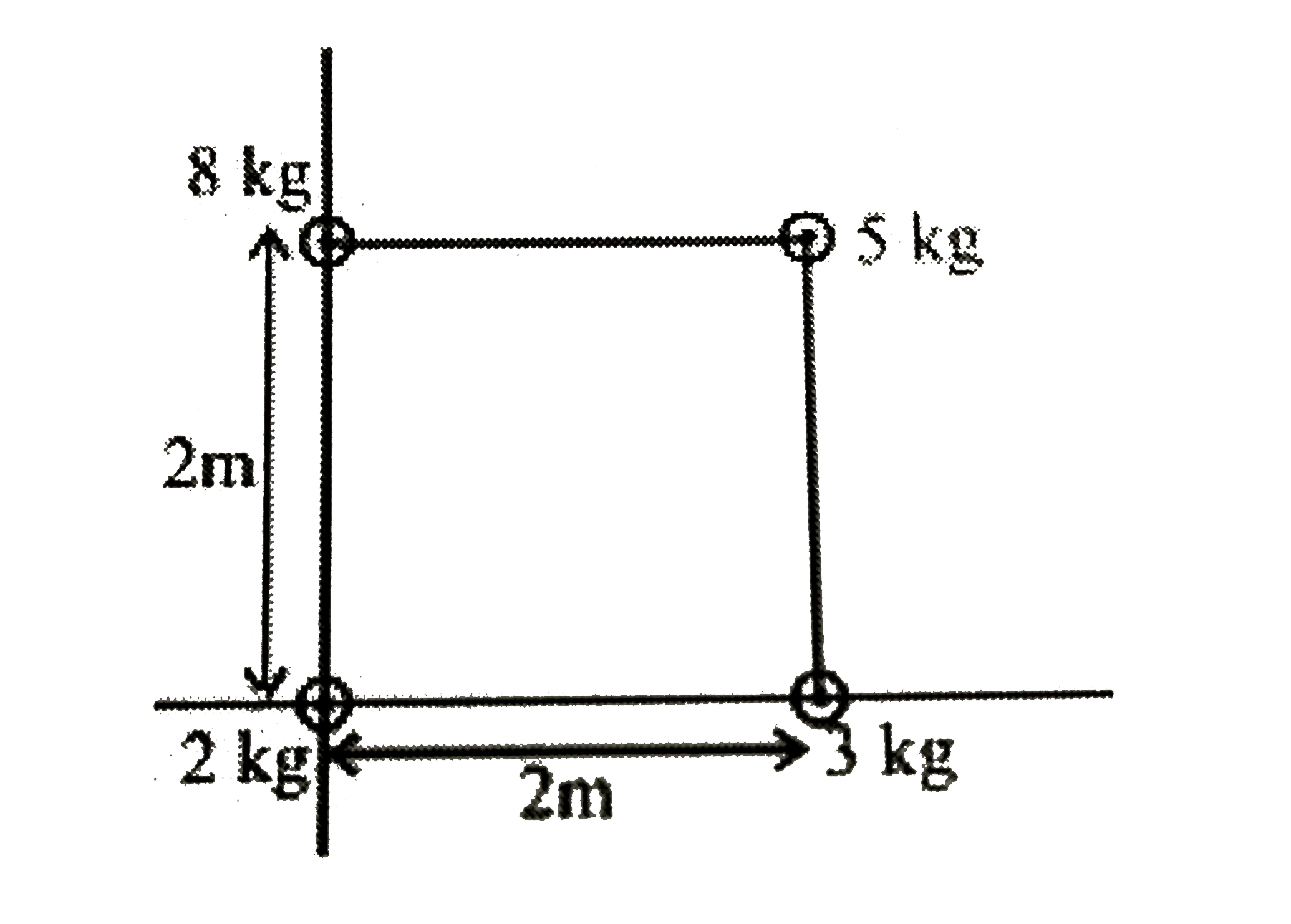
View SolutionCalculate centre of mass of the system
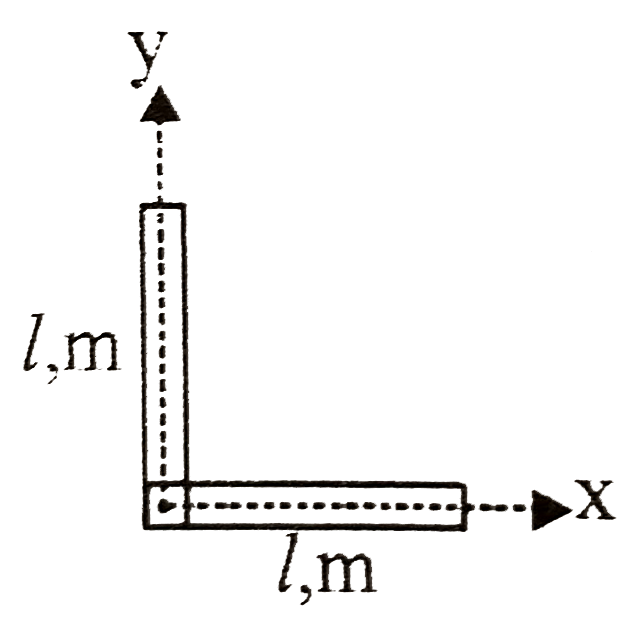
View SolutionWrite an expression for the centre of mass of& two partide system
View SolutionWhat is the position vector of centre of mass of two particles of equal masses ?
View Solution
