Write an expression for the velocity of the centre of mass of a system of particles.
To derive the expression for the velocity of the center of mass of a system of particles, we can follow these steps:
Step 1: Define the System of Particles
Consider a system of N particles, where each particle i has a mass mi and a position vector →ri.
Step 2: Define the Center of Mass
The position of the center of mass →Rcm of the system is given by the formula:
→Rcm=1MN∑i=1mi→ri
where M is the total mass of the system, defined as:
M=N∑i=1mi
Step 3: Differentiate the Center of Mass Position
To find the velocity of the center of mass →Vcm, we differentiate the position of the center of mass with respect to time:
→Vcm=d→Rcmdt
Step 4: Apply the Derivative to the Center of Mass Equation
Using the expression for →Rcm, we can differentiate:
→Vcm=1MN∑i=1mid→ridt
Here, d→ridt is the velocity of the i-th particle, denoted as →vi.
Step 5: Substitute and Simplify
Thus, we can rewrite the expression for the velocity of the center of mass:
→Vcm=1MN∑i=1mi→vi
Final Expression
The final expression for the velocity of the center of mass of a system of particles is:
→Vcm=∑Ni=1mi→vi∑Ni=1mi
Consider a system of N particles, where each particle i has a mass mi and a position vector →ri.
The position of the center of mass →Rcm of the system is given by the formula:
→Rcm=1MN∑i=1mi→ri
where M is the total mass of the system, defined as:
M=N∑i=1mi
To find the velocity of the center of mass →Vcm, we differentiate the position of the center of mass with respect to time:
→Vcm=d→Rcmdt
Using the expression for →Rcm, we can differentiate:
→Vcm=1MN∑i=1mid→ridt
Here, d→ridt is the velocity of the i-th particle, denoted as →vi.
Thus, we can rewrite the expression for the velocity of the center of mass:
→Vcm=1MN∑i=1mi→vi
The final expression for the velocity of the center of mass of a system of particles is:
→Vcm=∑Ni=1mi→vi∑Ni=1mi
Topper's Solved these Questions
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
Similar Questions
Knowledge Check
The centre of mass of a system of particles does not depend on
AMasses of the particlesBForces on the particles,CPosition of the particlesDRelative distance between the particles.The centre of mass of a system of particles does not depend on
Amasses of the particlesBforces acting on the particlesCposition of the particlesDrelative distances between the particles
Obtain an expression for the position vector of centre of mass of a two particle system.
View SolutionCalculate centre of mass of the system
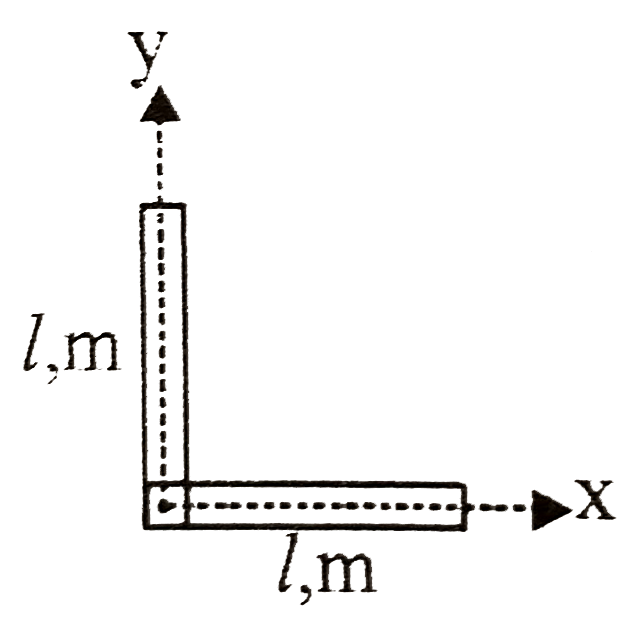
View SolutionThree identical particles, each of mass m, are located in space at the vertices of an equilateral triangle of side length a. They are revolving in a circular orbital under mutual ravitational attraction. Find the speed of each particle. Find the acceleration of the centre of mass of a system comprising of any two particles. Assume that one of the particles suddenly loses its ability to exert gravitational force. Find the velocity of the centre of mass of the system of other two particles after this.
View SolutionWrite an expression for the centre of mass of& two partide system
View SolutionQuestions on centre of mass of system of particle and bodies
View SolutionCalculate the velocity of the centre of mss of the system of particles shown in figure.
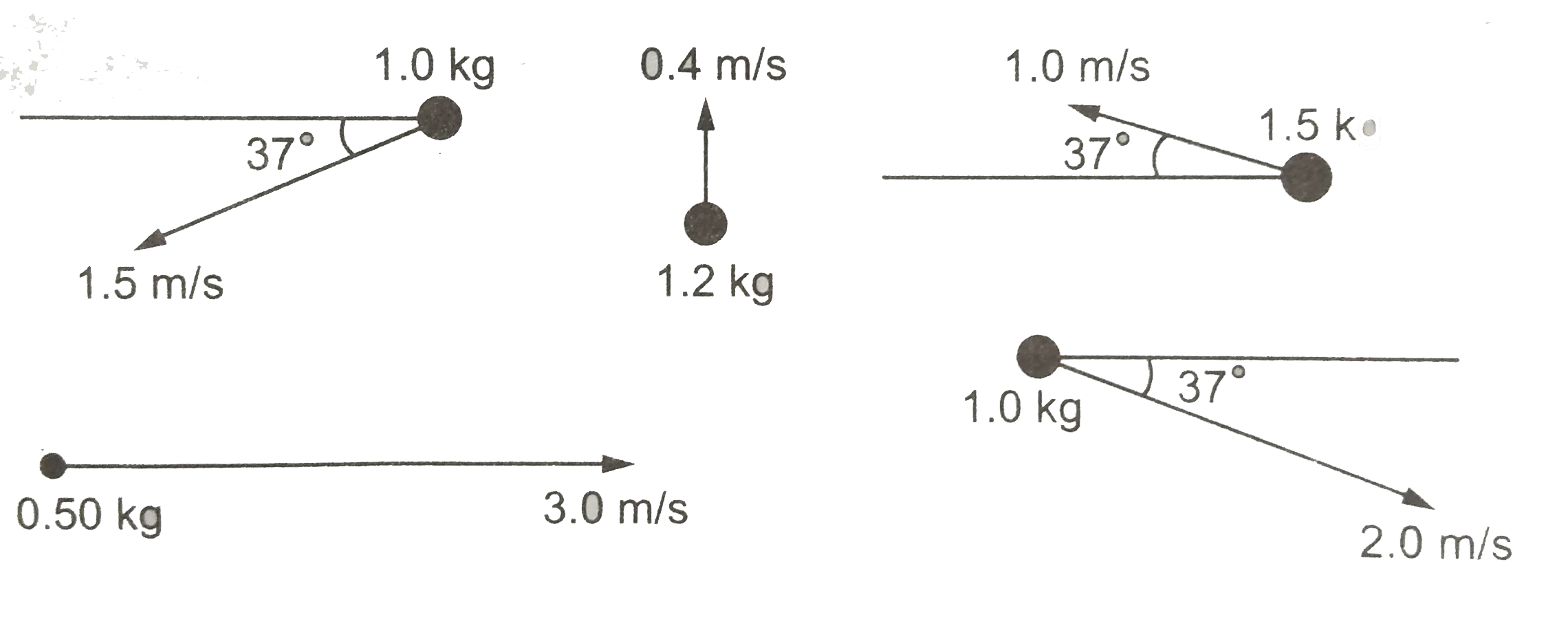
View Solution
