Show that in the absence of any external force, the velocity of the centre of mass remains constant.
To show that in the absence of any external force, the velocity of the center of mass remains constant, we can follow these steps:
Step 1: Understand the Concept of Center of Mass
The center of mass (CM) of a system of particles is defined as the point where the total mass of the system can be considered to be concentrated. The position of the center of mass →Rcm for a system of n particles is given by:
→Rcm=1Mn∑i=1mi→ri
where M is the total mass of the system, mi is the mass of the ith particle, and →ri is the position vector of the ith particle.
Step 2: Apply Newton's Second Law
According to Newton's second law, the net external force →Fext acting on a system is equal to the rate of change of momentum of the system:
→Fext=d→Pdt
where →P is the total momentum of the system.
Step 3: Consider the Case of Zero External Force
If there is no external force acting on the system, we have:
→Fext=0
This implies:
d→Pdt=0
Step 4: Analyze the Total Momentum
The total momentum →P of the system can be expressed as:
→P=n∑i=1mi→vi
where →vi is the velocity of the ith particle. Since the rate of change of total momentum is zero, we conclude that:
d→Pdt=0⟹→P=constant
Step 5: Relate Momentum to Center of Mass Velocity
The momentum of the center of mass can also be expressed as:
→P=M→Vcm
where →Vcm is the velocity of the center of mass, and M is the total mass of the system. Since →P is constant, we have:
M→Vcm=constant
Step 6: Conclude the Velocity of Center of Mass
Since the total mass M is constant (assuming no mass is added or removed from the system), it follows that:
→Vcm=→PM=constant
Thus, we conclude that in the absence of any external force, the velocity of the center of mass remains constant.
Summary
In summary, we have shown that if no external forces act on a system, the momentum of the system remains constant, leading to the conclusion that the velocity of the center of mass also remains constant.
---
The center of mass (CM) of a system of particles is defined as the point where the total mass of the system can be considered to be concentrated. The position of the center of mass →Rcm for a system of n particles is given by:
According to Newton's second law, the net external force →Fext acting on a system is equal to the rate of change of momentum of the system:
If there is no external force acting on the system, we have:
The total momentum →P of the system can be expressed as:
The momentum of the center of mass can also be expressed as:
Since the total mass M is constant (assuming no mass is added or removed from the system), it follows that:
In summary, we have shown that if no external forces act on a system, the momentum of the system remains constant, leading to the conclusion that the velocity of the center of mass also remains constant.
Topper's Solved these Questions
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
Similar Questions
Knowledge Check
Assertion : If there is no external torque on a body about its centre of mass, then the velocity of the centre of mass remains constant.
Reason : The linear momentum of an isolated system remains constant.AIf both, Assertion and Reason are true and the Reason is the correct explanation of the Assertion.BIf both, Assertion and Reason are true but Reason is not a correct explanation of the Assertion.CIf Assertion is true but the Reason is false.DIf both, Assertion and Reason are false.Satement-1: if there is no external torque on a body about its centre of mass, then the velocity of the center of mass remains constant.
Statement-2: The linear momentum of an isolated system remains constant.AStatement-1 is true Statement -2 is True, Statement-2 is a correct explanation for Statement -1BStatement -1 is True, Statement -2 is True, Statement-2 is NOT a correct explanation for Statement -1CStatement-1 is True, Statement-2 is FalseDStatement -1 is False, Statement-2 is TrueStatement 1: Two spheres undergo a perfectly elastic collision. The kinetic energy of system of both spheres is always constant. [There is no external force on system of both spheres]. Statement 2: If net external force on a system is zero, the velocity of centre of mass remains constant.
AStatement-1 is true, Statement-2: is true, Statement-2 is a correct explanation for Statement-1.BStatement-1 is true, Statement-2: is true, Statement-2 is NOT a correct explanation for Statement-1.CStatement-1 is true but statement-2 is falseDStatement-1 is false, Statement-2 is true
Which of the following is true for center of mass ?
(i) The center of mass of a body may lie within , outside , on the surface of the body.
(ii) In the case of symmetrical bodies , the center of mass coincides with the geometrical center of the body.
(iii) In the absence of external forces , the center of mass moves with constant velocity.
(iv) If external forces are absent and system is initially at rest, then location of center of mass is fixed.
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

Find the relative velocity of the blocks after 'm' leaves contact with the spring.
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

What is the loss in the energy of the system due to breaking of B?
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

Now m arrives at B. Due to its inertia of motion 'm' breaks the support 'B' and due to some resistance offered by 'B' , the resulting velocity of 'm' is reduced to half of its previous value. Then what you can say about the velocity of 2m?
View SolutionAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.
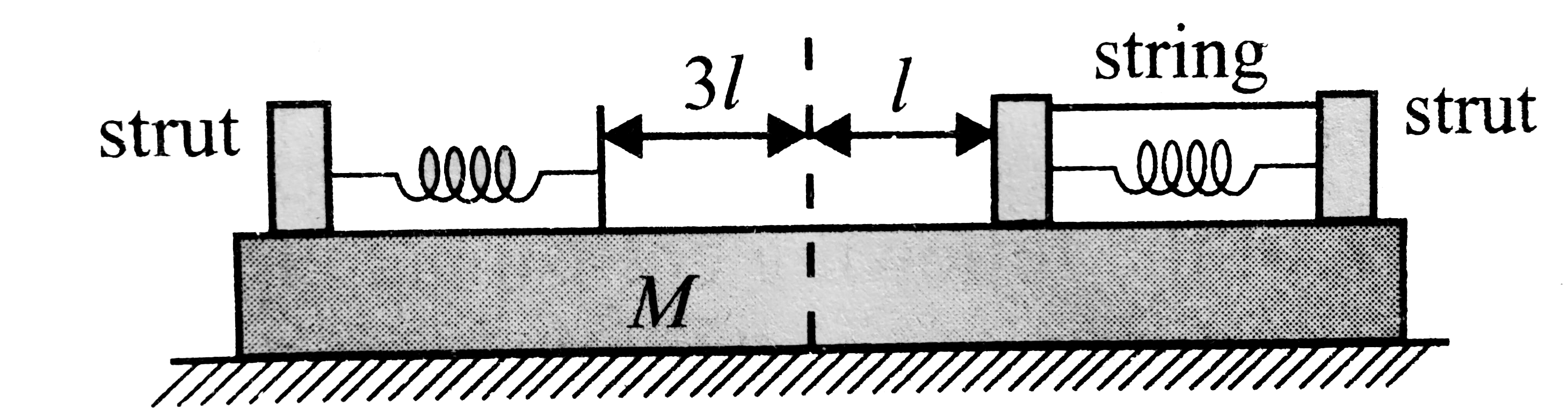
The maximum velocity of the plank is
View Solution
