Draw graphs showing the variation of acceleration due to gravity with depth below the earth's surface.
To draw the graph showing the variation of acceleration due to gravity (g') with depth (x) below the Earth's surface, we can follow these steps:
Step 1: Understand the relationship
The acceleration due to gravity at a depth x below the Earth's surface is given by the formula:
g′=g(1−xR)
where:
- g′ is the acceleration due to gravity at depth x,
- g is the acceleration due to gravity at the Earth's surface,
- R is the radius of the Earth,
- x is the depth below the Earth's surface.
Step 2: Identify key points
1. At the surface (x = 0):
- g′=g
2. At the center of the Earth (x = R):
- g′=0
Step 3: Plot the points
- When x=0, g′=g (this is the starting point of the graph).
- When x=R, g′=0 (this is the endpoint of the graph).
Step 4: Draw the graph
1. Draw the x-axis representing the depth below the Earth's surface (x).
2. Draw the y-axis representing the acceleration due to gravity (g').
3. Mark the point (0, g) on the y-axis.
4. Mark the point (R, 0) on the x-axis.
5. Connect these two points with a straight line, indicating that as depth increases, the acceleration due to gravity decreases linearly.
Step 5: Label the graph
- Label the y-axis as "Acceleration due to gravity (g')" and the x-axis as "Depth below the Earth's surface (x)".
- Mark the point where the graph intersects the y-axis as g and the point where it intersects the x-axis as R.
Final Graph
The graph will be a straight line starting from the point (0, g) and ending at the point (R, 0), showing a linear decrease in acceleration due to gravity with increasing depth below the Earth's surface.
---
The acceleration due to gravity at a depth x below the Earth's surface is given by the formula:
g′=g(1−xR)
where:
- g′ is the acceleration due to gravity at depth x,
- g is the acceleration due to gravity at the Earth's surface,
- R is the radius of the Earth,
- x is the depth below the Earth's surface.
1. At the surface (x = 0):
- g′=g
2. At the center of the Earth (x = R):
- g′=0
- When x=0, g′=g (this is the starting point of the graph).
- When x=R, g′=0 (this is the endpoint of the graph).
1. Draw the x-axis representing the depth below the Earth's surface (x).
2. Draw the y-axis representing the acceleration due to gravity (g').
3. Mark the point (0, g) on the y-axis.
4. Mark the point (R, 0) on the x-axis.
5. Connect these two points with a straight line, indicating that as depth increases, the acceleration due to gravity decreases linearly.
- Label the y-axis as "Acceleration due to gravity (g')" and the x-axis as "Depth below the Earth's surface (x)".
- Mark the point where the graph intersects the y-axis as g and the point where it intersects the x-axis as R.
The graph will be a straight line starting from the point (0, g) and ending at the point (R, 0), showing a linear decrease in acceleration due to gravity with increasing depth below the Earth's surface.
Topper's Solved these Questions
Similar Questions
Draw graphs showing the variation of accleeration due to gravity with (a) height above the Earth's surface, (b) depth below the Earth's surface.
View SolutionDraw graphs showing the variation of accleeration due to gravity with (a) height above the Earth's surface, (b) depth below the Earth's surface.
View Solution
Knowledge Check
Which of the following graphs shows the variation of acceleration due to gravity g with depth h from the surface of the earth ?
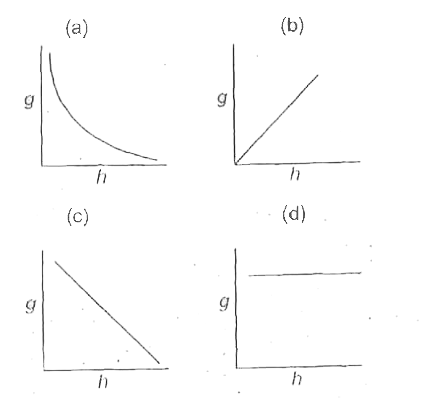 A(a)B(b)C(c )D(d)
A(a)B(b)C(c )D(d)
Variation In Acceleration Due To Gravity
View SolutionDerive an expression for the acceleration due to gravity at a depth d below the Earth's surface.
View SolutionDraw graphs showing the variation of accleeration due to gravity with (a) height above the Earth's surface, (b) depth below the Earth's surface.
View SolutionWhich of the following graphs shows an approximate variation of acceleration due to gravity g with height h above the Earth's surface?

View SolutionLet g be the acceleration due to gravity on the earth's surface.

View SolutionThe acceleration due to gravity at a depth R/2 below the surface of the earth is
View SolutionDoes the concentration of the earth's mass near its centre change the variation of g (acceleration due to gravity) with height from its surface?
View Solution
