A body of weight mg is hanging on a string which extends in length by I. The work done in extending the string is
mgl
mgl/2
2 mgl
none of these
To find the work done in extending a string by a length l when a weight mg is hung from it, we can follow these steps:
Step 1: Understand the Setup
We have a string (or wire) of original length L that is fixed at one end. When a weight mg is hung from the other end, the string stretches by an amount l.
Step 2: Define the Force
The force applied to the string due to the weight is F=mg.
Step 3: Determine the Relationship Between Stress and Strain
Using Young's modulus Y, we know that:
Y=StressStrain=F/AΔL/L
where A is the cross-sectional area of the string, ΔL is the elongation (which is l), and L is the original length of the string.
Step 4: Express Force in Terms of Elongation
From the definition of Young's modulus, we can rearrange the equation to express the force:
F=Y⋅A⋅lL
Step 5: Calculate Work Done
The work done W in stretching the string can be calculated by integrating the force over the distance stretched. Since the force changes as the string stretches, we need to integrate:
W=∫l0Fdx
Substituting F from the previous step, we have:
W=∫l0(Y⋅A⋅xL)dx
Step 6: Perform the Integration
The integral becomes:
W=Y⋅AL∫l0xdx
The integral of x from 0 to l is:
∫l0xdx=l22
Thus, we have:
W=Y⋅AL⋅l22
Step 7: Substitute Young's Modulus
Now, substituting Y back into the equation:
Y=mg⋅LA⋅l
We can replace Y in the work done equation:
W=(mg⋅L/A⋅l)⋅AL⋅l22
This simplifies to:
W=mg⋅l2
Final Answer
Therefore, the work done in extending the string by a length l is:
W=mg⋅l2
---
We have a string (or wire) of original length L that is fixed at one end. When a weight mg is hung from the other end, the string stretches by an amount l.
The force applied to the string due to the weight is F=mg.
Using Young's modulus Y, we know that:
Y=StressStrain=F/AΔL/L
where A is the cross-sectional area of the string, ΔL is the elongation (which is l), and L is the original length of the string.
From the definition of Young's modulus, we can rearrange the equation to express the force:
F=Y⋅A⋅lL
The work done W in stretching the string can be calculated by integrating the force over the distance stretched. Since the force changes as the string stretches, we need to integrate:
W=∫l0Fdx
Substituting F from the previous step, we have:
W=∫l0(Y⋅A⋅xL)dx
The integral becomes:
W=Y⋅AL∫l0xdx
The integral of x from 0 to l is:
∫l0xdx=l22
Thus, we have:
W=Y⋅AL⋅l22
Now, substituting Y back into the equation:
Y=mg⋅LA⋅l
We can replace Y in the work done equation:
W=(mg⋅L/A⋅l)⋅AL⋅l22
This simplifies to:
W=mg⋅l2
Therefore, the work done in extending the string by a length l is:
W=mg⋅l2
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - Mechanical Properties of SolidsEXERCISE - Example113videos
Mechanical Properties of Solids
- BOOK - SL ARORACHAPTER - Mechanical Properties of fluidsEXERCISE - Exercise459videos
Mechanical Properties of fluids
- BOOK - SL ARORACHAPTER - MECHANICSEXERCISE - Exercise341videos
MECHANICS
Similar Questions
A body of mass M is hanging by an inextensible string of mass m. If the free end of the string accelerates up with constant acceleration a. find the variation of tension in the string a fuction of the distance measured from the mass M (bottom of the string).
 View Solution
View SolutionThree equal weights of mass m each are hanging on a string passing over a fixed pulley as shown in fig. The tensions in the string connecting weights A to B and B to C will respectively be -
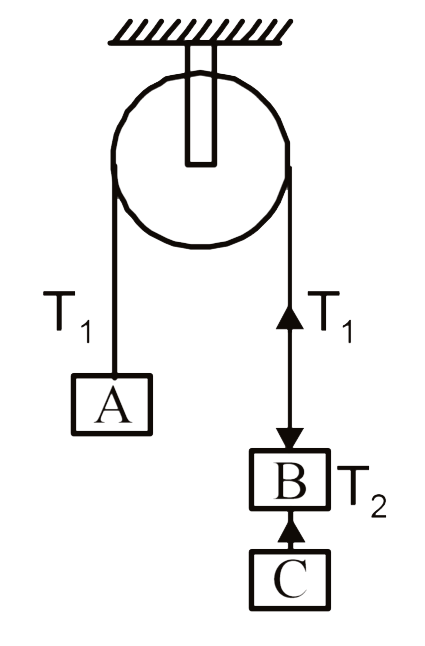 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
When a stone tied to a string is whirled in a circle, the work done on it by the string is
ApositiveBnegativeCzeroDundefined - Question 2 - Select One
STATEMENT-1: An elastic spring of force constant k is stretched by a small length x. The work done in extending the spring by a further length x is 2kx2.
because
STATEMENT-2: The work done in extending an elastic spring by a length x is proportional to x2.AStatement-1 is true, Statement-2 is True, Statement -2 is a correct explanation for Statement-1.BStatement-1 is True, Statement-2 is True, Statement -2 is NOT a correct explanation for Statement-1.CStatement-1 is True, Statement-2 is False.DStatement - 1 is False, Statement -2 is True. - Question 3 - Select One
If a wire is extended to a new length , the L, the work done is
AYAl(l−l)BYAl(l−l)2C12YAl(l−l')2DYAl(l−l)2
A block of mass M hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F. The kinetic of the block increases by 40J in 1s. State whether the following statements are true or false.
(a) The tension in the string is Mg .
(b) The work done the tension on the block is 40J.
(c) the tension in the string is F.
(d) The work done by the force of gravity is 40J in the above 1s .View SolutionA body of mass m is allowed to fall with the help of string with downward acceleration g/6 to distance x. The work done by the string is
View Solutionwhen the bob of a simple pendulum swings, the work done by bob in the string is :
View SolutionIf a spring is extended to length l, the according to Hook's law
View SolutionA body of mass m is allowed to fall with the help of string with downward acceleration g6 to a distance x. The work done by the string is
View Solution

