A body of mass M is hanging by an inextensible string of mass m. If the free end of the string accelerates up with constant acceleration a. find the variation of tension in the string a fuction of the distance measured from the mass M (bottom of the string).

Let T be the tension in the string at a distance x from its bottom. Referring to the FBD, we have the following equations:
Force equation for (m1):
T=m1g−Mg=(M+m1)a …(i)
We are writing equation of motion for lower parts as we are not given the force acting on top of the string.
Substituting m1=mlx in equation (i), we have
T=(M+mxl)(g+a)
At x=l,T=(M+m)(g+a)=F(say)
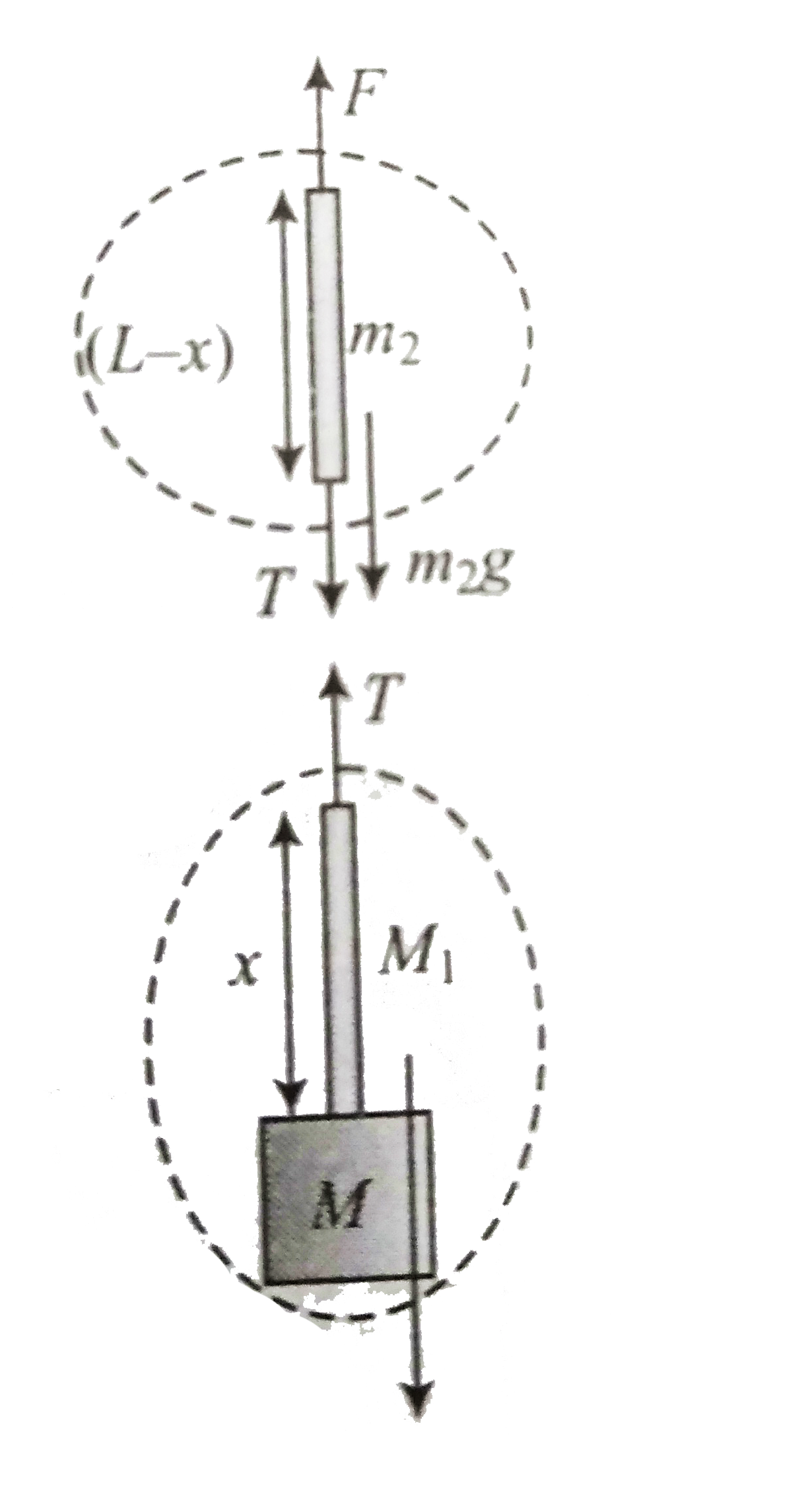
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
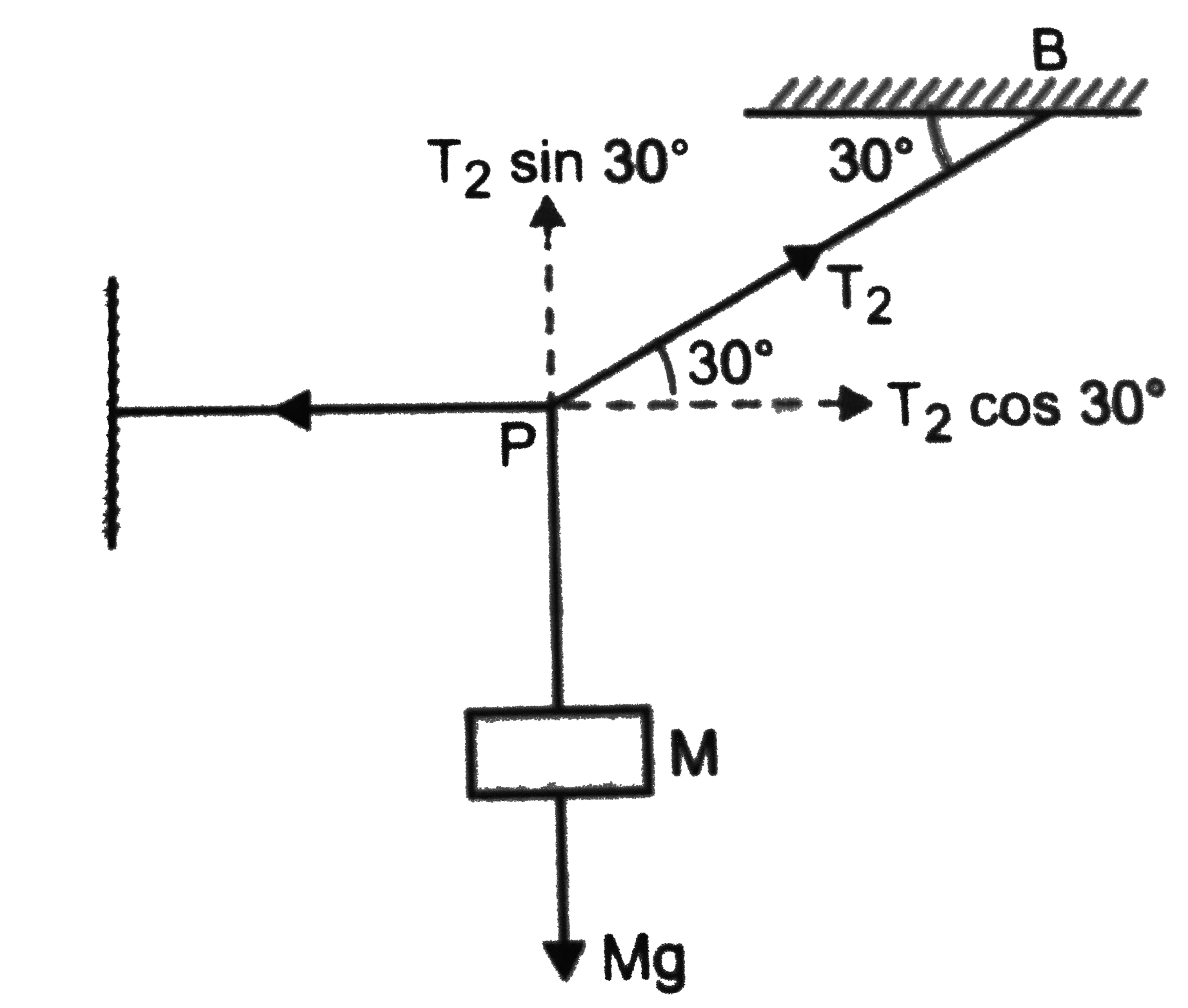
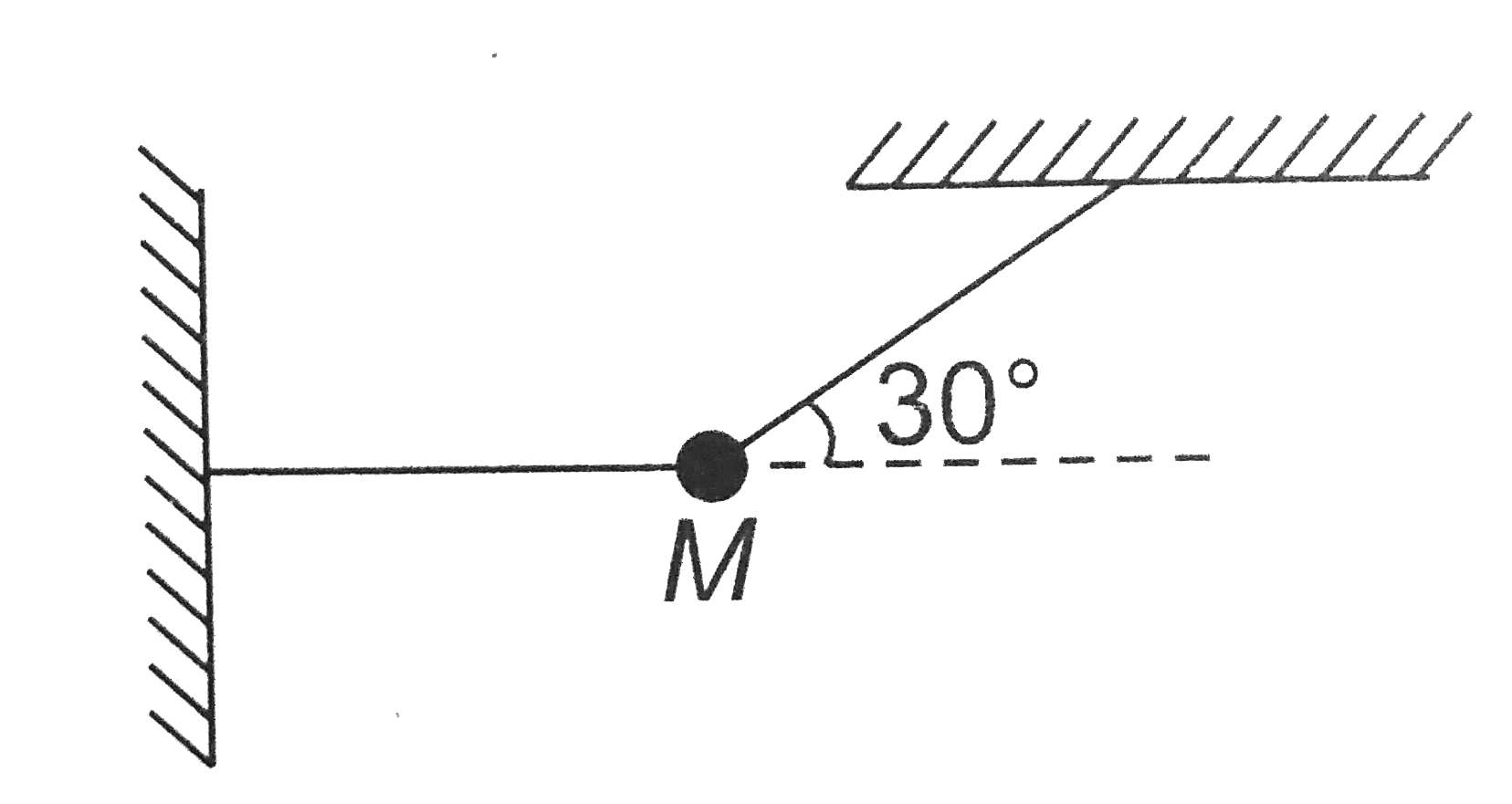
A mass M is hung with a light inextensible string as shown in Find the tension in the horizontal part of the string .
 View Solution
View SolutionA small metallic sphere of mass m is suspended from the ceiling of a car accelerating on a horizontal road with constant acceleration a. The tension in the string attached with metallic sphere is
View Solution
Knowledge Check
- Question 1 - Select One
A mass M is hung with a light inextensible string. Tension in horizontal part of string is.
 A√3MgB√2MgCmg√3Dmg2
A√3MgB√2MgCmg√3Dmg2 - Question 2 - Select One
A mass of 1 kg is supended by a string. It is
(i) lifted up with an acceleration 4.9m/s2
(ii) lowered with an acceleration 4.9m/s2
Then the ration of the tension in the string in the two cases isA3:1B1:3C2:1D1:2 - Question 3 - Select One
The block of mass m is at rest. Find the tension in the string A .
 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mg
A mass of 1kg attached to one end of a string is first lifted up with an acceleration 4.9m/s2 and then lowered with same acceleration What is the ratio of tension in string in two cases .
View SolutionA block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
View SolutionA mass M is lowered with the help of a string by a distance h at a distance acceleration g/2. The work done by the string will be
View SolutionA body of mass M is being pulled by a string of mass m with a force P applied at one end. The force exerted by the string on the body is
View SolutionA string is used to pull a block of mass m vertically up by a distance h at a constant acceleration g3. The work done by the tension in the string is
View Solution

