Define stress and strain and derive their units. What is Hooke's law? Write its one limitation.
Step-by-Step Solution:
Step 1: Define Stress
Stress is defined as the force applied per unit area of a material. Mathematically, it can be expressed as:
Stress=ForceArea
Where:
- Force is measured in Newtons (N)
- Area is measured in square meters (m²)
Step 2: Derive the Unit of Stress
From the definition of stress, we can derive its unit:
Unit of Stress=Unit of ForceUnit of Area=Nm2
Thus, the unit of stress is:
N/m2 or Pascal (Pa)
Step 3: Define Strain
Strain is defined as the ratio of the change in a particular quantity (such as length, volume, or area) to the original value of that quantity. For example, if we consider length, strain can be expressed as:
Strain=Change in LengthOriginal Length=ΔLL0
Where:
- ΔL is the change in length (final length - initial length)
- L0 is the original length
Step 4: Derive the Unit of Strain
Since strain is a ratio of two lengths, it is dimensionless:
Unit of Strain=MeterMeter=1 (unitless)
Step 5: State Hooke's Law
Hooke's Law states that the stress applied to a material is directly proportional to the strain produced in that material, as long as the material is within its elastic limit. Mathematically, it can be expressed as:
Stress∝Strain
Or, when we introduce a proportionality constant (Young's modulus, E):
Stress=E⋅Strain
Step 6: State One Limitation of Hooke's Law
One limitation of Hooke's Law is that it is only valid for small deformations. When the deformation becomes large, the relationship between stress and strain may no longer be linear, and Hooke's Law does not apply.
Stress is defined as the force applied per unit area of a material. Mathematically, it can be expressed as:
Stress=ForceArea
Where:
- Force is measured in Newtons (N)
- Area is measured in square meters (m²)
From the definition of stress, we can derive its unit:
Unit of Stress=Unit of ForceUnit of Area=Nm2
Thus, the unit of stress is:
N/m2 or Pascal (Pa)
Strain is defined as the ratio of the change in a particular quantity (such as length, volume, or area) to the original value of that quantity. For example, if we consider length, strain can be expressed as:
Strain=Change in LengthOriginal Length=ΔLL0
Where:
- ΔL is the change in length (final length - initial length)
- L0 is the original length
Since strain is a ratio of two lengths, it is dimensionless:
Unit of Strain=MeterMeter=1 (unitless)
Hooke's Law states that the stress applied to a material is directly proportional to the strain produced in that material, as long as the material is within its elastic limit. Mathematically, it can be expressed as:
Stress∝Strain
Or, when we introduce a proportionality constant (Young's modulus, E):
Stress=E⋅Strain
One limitation of Hooke's Law is that it is only valid for small deformations. When the deformation becomes large, the relationship between stress and strain may no longer be linear, and Hooke's Law does not apply.
Topper's Solved these Questions
- Mechanical Properties of SolidsBOOK - SL ARORACHAPTER - Mechanical Properties of SolidsEXERCISE - Example
113 Videos
- Mechanical Properties of fluidsBOOK - SL ARORACHAPTER - Mechanical Properties of fluidsEXERCISE - Exercise
459 Videos
- MECHANICSBOOK - SL ARORACHAPTER - MECHANICSEXERCISE - Exercise
341 Videos
Similar Questions
Knowledge Check
Hook's law defines
AstressBstrainCmodulus of elasticityDelastic limitHook's law defines
AStressBStrainCModulus of elasticityDElastic limitA graph is shown between stress and strain for a metal. The part in which Hooke's law holds good is
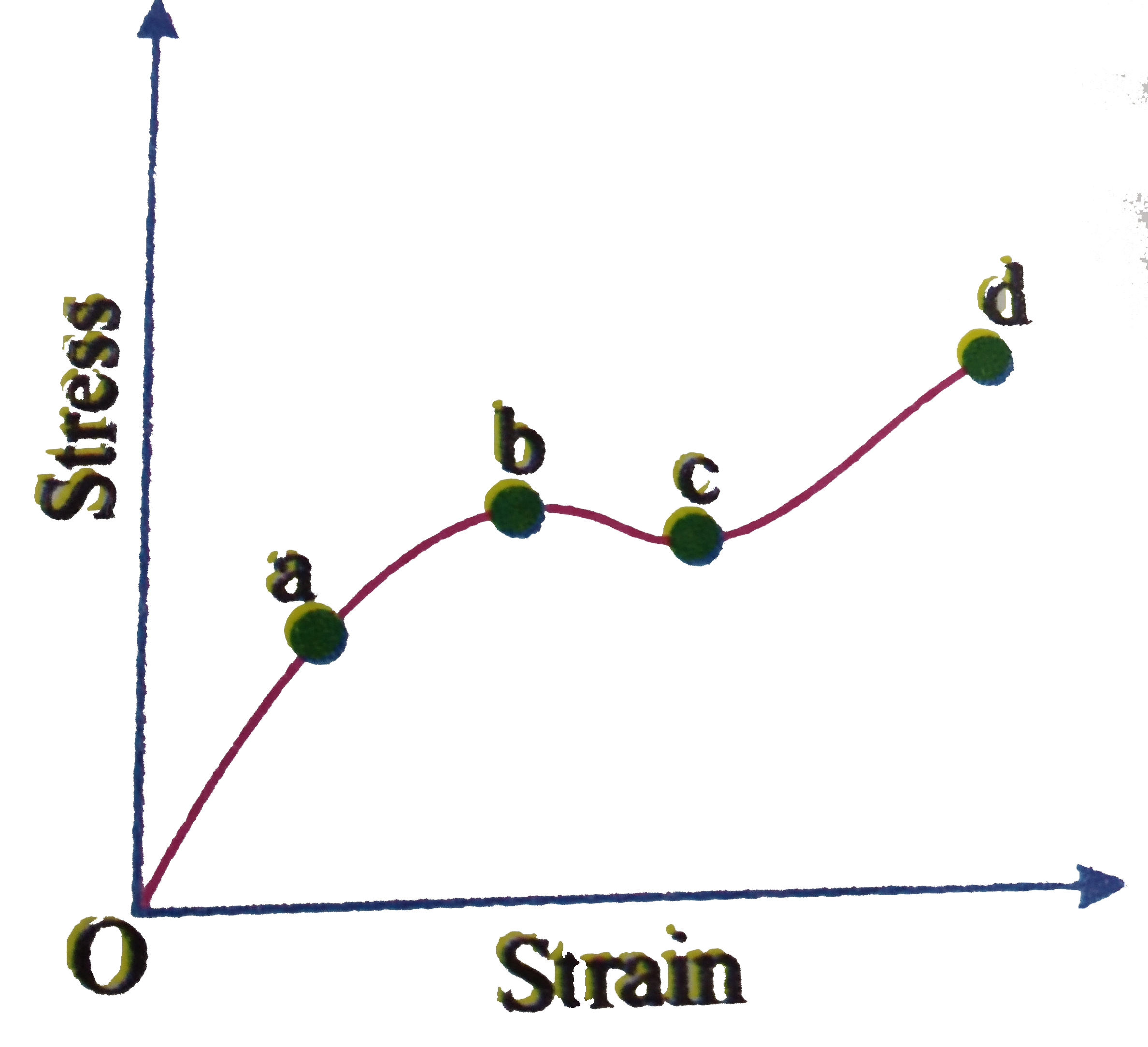 AOABABCBCDOD
AOABABCBCDOD
Define mutual inductance and write its S.I. units.
View SolutionDefine power of a lens and write its SI unit.
View SolutionDefine octet rule. Write its significance and limitations.
View SolutionDefine ebullioscopic constant. Write its unit.
View SolutionA graph is shown between stress and strain for a metal. The part in which Hooke's law holds good is

View Solution
