Describe the various modes of vibrations of an open organ pipe.
To describe the various modes of vibrations of an open organ pipe, we need to understand the fundamental principles of wave motion and resonance in such a system. Here’s a step-by-step breakdown of the modes of vibration:
Step 1: Understanding the Structure of an Open Organ Pipe
An open organ pipe is a tube that is open at both ends. This means that at both ends of the pipe, the air can move freely, resulting in antinodes (points of maximum amplitude) at both ends.
Hint: Remember that antinodes occur at open ends, while nodes (points of zero amplitude) occur at closed ends.
Step 2: Fundamental Mode of Vibration (First Harmonic)
The simplest mode of vibration is the fundamental mode, also known as the first harmonic. In this mode, the length of the pipe (L) supports one complete wave, which consists of two antinodes at the ends and one node in the middle. The wavelength (λ) in this case is twice the length of the pipe.
- Wavelength (λ) = 2L
- Frequency (f) = V / λ = V / (2L)
Hint: The fundamental mode is the lowest frequency mode and has the longest wavelength.
Step 3: First Overtone (Second Harmonic)
The first overtone is the second harmonic. In this mode, there are two complete waves fitting into the length of the pipe. This results in three antinodes (two at the ends and one in the middle) and two nodes (one in between the two antinodes).
- Wavelength (λ) = L
- Frequency (f) = V / λ = V / L
Hint: The first overtone has a higher frequency than the fundamental mode and fits more waves into the same length.
Step 4: Second Overtone (Third Harmonic)
The second overtone is the third harmonic. In this mode, there are three complete waves fitting into the length of the pipe. This results in four antinodes and three nodes.
- Wavelength (λ) = (2/3)L
- Frequency (f) = V / λ = 3V / (2L)
Hint: Each subsequent harmonic adds an additional node and antinode, increasing the frequency.
Step 5: General Formula for Harmonics
The general formula for the frequency of the nth harmonic in an open organ pipe can be expressed as:
- Frequency (f_n) = nV / (2L)
Where:
- n = harmonic number (1 for fundamental, 2 for first overtone, 3 for second overtone, etc.)
- V = speed of sound in air
- L = length of the pipe
Hint: The harmonic number (n) determines the mode of vibration and directly affects the frequency.
Summary
In summary, an open organ pipe can produce multiple modes of vibration:
1. Fundamental Mode (1st Harmonic): One wave, frequency = V / (2L)
2. First Overtone (2nd Harmonic): Two waves, frequency = V / L
3. Second Overtone (3rd Harmonic): Three waves, frequency = 3V / (2L)
Each mode corresponds to a specific harmonic number and has a distinct frequency determined by the length of the pipe and the speed of sound.
An open organ pipe is a tube that is open at both ends. This means that at both ends of the pipe, the air can move freely, resulting in antinodes (points of maximum amplitude) at both ends.
The simplest mode of vibration is the fundamental mode, also known as the first harmonic. In this mode, the length of the pipe (L) supports one complete wave, which consists of two antinodes at the ends and one node in the middle. The wavelength (λ) in this case is twice the length of the pipe.
- Frequency (f) = V / λ = V / (2L)
The first overtone is the second harmonic. In this mode, there are two complete waves fitting into the length of the pipe. This results in three antinodes (two at the ends and one in the middle) and two nodes (one in between the two antinodes).
- Frequency (f) = V / λ = V / L
The second overtone is the third harmonic. In this mode, there are three complete waves fitting into the length of the pipe. This results in four antinodes and three nodes.
- Frequency (f) = V / λ = 3V / (2L)
The general formula for the frequency of the nth harmonic in an open organ pipe can be expressed as:
- n = harmonic number (1 for fundamental, 2 for first overtone, 3 for second overtone, etc.)
- V = speed of sound in air
- L = length of the pipe
In summary, an open organ pipe can produce multiple modes of vibration:
1. Fundamental Mode (1st Harmonic): One wave, frequency = V / (2L)
2. First Overtone (2nd Harmonic): Two waves, frequency = V / L
3. Second Overtone (3rd Harmonic): Three waves, frequency = 3V / (2L)
Topper's Solved these Questions
Similar Questions
Knowledge Check
Modes of vibration in an open organ pipe are represented by –
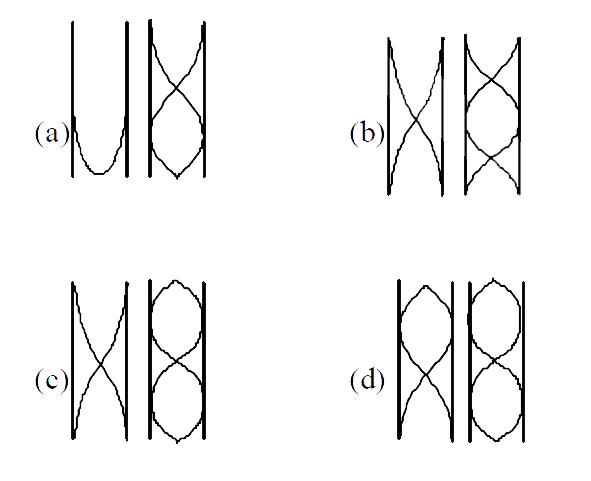 AaBbCcDd
AaBbCcDdThe frequency of vibration of open orgen pipe is
Av4lBv2l+1.2dCvlDv8lAssertion: The fundamental frequency of vibration of an open organ pipe remains same if the radius of the pipe is doubled.
Reason: Frequency of vibration of an open organ pipe is independent of the radius of pipe.AAssertion is True, Reason is True, Reason is a correct explanation for AssertionBAssertion is True, Reason is True, Reason is not a correct explanation for AssertionCAssertion is True, Reason is FalseDAssertion is False but, Reason is True.
Discuss various modes of vibration in open ends organ pipe. Also, show that the ratio of frequencies of different harmonics with first harmonic in open pipe is 1:2:3.
View SolutionDiagrammatically show first two modes of vibrations in case of an open organ pipe and write the ratio of their frequencies
View SolutionDerive an expression for the nth mode of vibration in case of a closed end organ pipe. Hence give the value of v1:v2:v3.
View SolutionA tuning fork vibrats with frequnecy 256Hz and gives one beat per seond with the third normal mode of vibration of an open pipe. What is the length of the pipe (Speed of sound in air is 340ms−1)
View SolutionModes of vibration in a closed organ pipe are represented by –
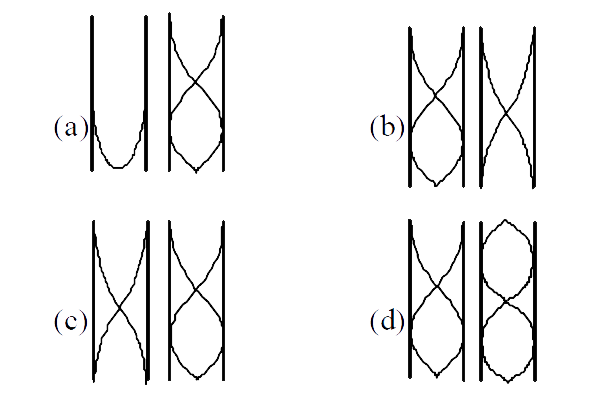
View Solution
