वृत्त x2+y2=16 के बिन्दुओं (4cosθ,4sinθ) तथा (4cos(θ+60∘),4sin(θ+60∘)) को जोड़ने वाली जीवा की लंबाई
16
2
4
8
The correct Answer is:C
Step by step video, text & image solution for वृत्त x^(2)+y^(2)=16 के बिन्दुओं (4cos theta, 4 sin theta) तथा (4cos(theta+60^(@)), 4sin(theta+60^(@))) को जोड़ने वाली जीवा की लंबाई by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (More than one correct answers)28videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Reasoning type questions )8videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - Solved Multiple Choice Questions (वृत्त की स्पर्श रेखा तथा अभिलम्ब)72videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वर्ग समीकरण एवं असमिकायें EXERCISE - JEE Advanced (Matrix Match type questions)2videos
वर्ग समीकरण एवं असमिकायें
- BOOK - ERRORLESS HINDICHAPTER - शांकव परिच्छेद EXERCISE - JEE Advanced (Matrix Match type questions)7videos
शांकव परिच्छेद
Similar Questions
माना कि L1 मूलबिन्दु से गुजरने वाली एक सरल रेखा है तथा सरल रेखा L2 का समीकरण x+y=1 है। यदि वृत्त x2+y2−x+3y=0 द्वारा L1 और L2 पर काटे गये अन्तःखण्ड बराबर हैं, तो निम्नलिखित में से कौन-सा समीकरण रेखा L1 को निरूपित करता है
05:58View Solutionमाना L1=2x+3y+p−3=0,L2:2x+3y+p+3=0
जहाँ p एक वास्तविक संख्या है तथा C=x2+y2+6x−10y+30=0
कथन-1 : यदि रेखा L1 वृत्त C की जीवा है, तब रेखा L2 सदैव वृत्त C का व्यास नही होगी तथा
कथन-2 : यदि रेखा L1 वृत्त C का व्यास है, तब रेखा L2 वृत्त C की जीवा नहीं होगी।03:48View Solutionरेखा lx+my+n=0 वृत्त x2+y2=a2 की एक स्पर्श रेखा होगी यदि
05:50View Solution
01:58View Solution
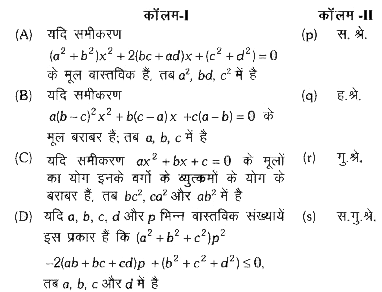
03:41View SolutionIf 3sin theta+4cos theta=5 then 4sin theta-3cos theta is equal to
02:34View SolutionIf 3cos theta+4cos theta=5 then 4sin theta-3cos theta is equal to
04:06View SolutionThe length ofthe chord joining the points (4cosθ,4sinθ) and [4cos(θ+60∘),4sin(θ+60∘)] of the circle x2+y2=16 is
05:24View Solutioncos(600−θ)cos(60∘+θ)=14(4cos2θ−3)
01:36View SolutionLet f(0)=sqrt(sin^(4)theta+4cos^(2)theta)-sqrt((cos^(4)theta)+4sin^(2)theta) ,then
01:34View SolutionIf (cos theta-4sin theta)=1 then (sin theta+4cos theta)=1)+-12)03 ) 24+-4
01:06View SolutionThe value of 3(cosθ−sinθ)4+6(sinθ+cosθ)2+4sin6θ is where θ∈(π4,π2) (a) 13−4cos4θ (b) 13−4cos6θ (c) 13−4cos6θ+2sin4θcos2θ (d) 13−4cos4θ+2sin4θcos2θ
05:01View SolutionThe length of the chord joining the points ( 4cosθ,4sinθ) and [4cos(θ+60∘),4sin(θ+60∘)] of the circle x2+y2=16 is :
08:03View Solution[cos2θ(3−4cos2θ)2+sin2θ(3−4sin2θ)2=
05:46View Solutioncos2θ(3−4cos2θ)2+sin2θ(4sin2θ−3)2=
07:25View Solution