Two blocks, of masses M and 2M are connected to a light spring of spring constant K that has one end fixed, a shown if fig. The blocks are released from the spring at its natural length codition.
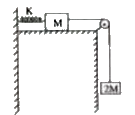
Maximum extention in the spring is 4MgK
Maximum Kinetic energy of the system is 2M2g2K
Maximum energy stored in the spring is four times that of maximum kinetic of the system.
When the kinetic energy of the system is maximum, energy stored in the spring is 4M2g2K
The correct Answer is:A, B, C
Topper's Solved these Questions
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE LEVEL -I(MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS
19 Videos
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED STRAIGHT OBJECTIVE TYPE QUESTIONS)
3 Videos
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - PRACTICE SHEET (EXERCISE-VII VERTICAL CIRCLE AND SPRINGS) (LEVEL -I STRAIGHT OBJECTIVE TYPE QUESTIONS)
11 Videos
- VISCOSITY BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers
3 Videos
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 3
61 Videos
Similar Questions
Two blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .
.
View SolutionTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .
.
View Solution
Knowledge Check
Two blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .AMaximum extension in the spring is 4MgK.BMaximum kinetic energy of the system is 2M2g2K.CMaximum energy stored in the spring is four times that of maximum kinetic energy of the system.DWhen kinetic energy of the system is maximum energy stored in the spring is 4M2g2K.
.AMaximum extension in the spring is 4MgK.BMaximum kinetic energy of the system is 2M2g2K.CMaximum energy stored in the spring is four times that of maximum kinetic energy of the system.DWhen kinetic energy of the system is maximum energy stored in the spring is 4M2g2K.Two blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
AF=μ(m1+m22)gBF=μ(m12+m2)gCF=μ(m21+m222)gDF=μ2(m21+m22)gTwo blocks are connected to the two free ends of a spring of spring constant K . Both the blocks are moved apart to extend the psring beyond its natural length and then released . In subsequent motion
AAccelerations of both the objects are equal and opposite of each other .BVelocities of both the bjects are equal and opposite of each other .CForces acting on both the objects are equal and opposite of each otherDLinear momenta of both the objects are equal and opposite of each other .
Two blocks of mass m and 2m are connected to a spring and wrapped around a smooth pulley as shown in the figure. Blocks are released together with spring in natural length. Calculate the maximum elongation (in meter) of the spring. Given mgK=3 meter.
View SolutionTwo blocks of masses m, and m, are connected to the ends of a spring of spring constant k. System is kept at rest on a frictionless horizontal floor with spring in its natural length. Both the blocks are pulled along opposite directions with forces of same magnitude F. Calculate maximum elongation of spring and distances travelled by the blocks during this motion.
View Solution
A block of mass m is pushed against a spring of spring constant k fixed at one end to a wall.The block can slide on a frictionless table as shown in the figure. The natural length of the spring is L0 and it is compressed to one fourth of natural length and the block is released.Find its velocity as a function of its distance (x) from the wall and maximum velocity of the block. The block is not attached to the spring.
View Solution
A block of mass m is pushed against a spring of spring constant k fixed at one end to a wall.The block can slide on a frictionless table as shown in the figure. The natural length of the spring is L0 and it is compressed to one fourth of natural length and the block is released.Find its velocity as a function of its distance (x) from the wall and maximum velocity of the block. The block is not attached to the spring.
View SolutionTwo blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.

View Solution
