A particle is projected along a horizontal field whose coefficient of friction varies as μ=A/r2, where r is the distance from the origin in metres and A is a positive constant. The initial distance of the particle 1m from the origin and its velocityy is radially outwards. the minimum initial velocity at this point so the particle never stops is √kgA. Find k.Solution in Telugu
The correct Answer is:2
Step by step video, text & image solution for A particle is projected along a horizontal field whose coefficient of friction varies as mu=A//r^(2), where r is the distance from the origin in metres and A is a positive constant. The initial distance of the particle 1m from the origin and its velocityy is radially outwards. the minimum initial velocity at this point so the particle never stops is sqrt(kgA). Find k. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - PRACTICE SHEET (ADVANCED) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
36 Videos
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED MATRIX MATCHING TYPE QUESTIONS)
1 Videos
- VISCOSITY BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers
3 Videos
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 3
61 Videos
Similar Questions
The velocity of a particle of mass 10−2kg is given as →v=(2xˆu+3yˆj+4zˆk) m/sec (where x, y and z are in meter). The amount of work done by applied force in displacing a particle from (1m, 2m, 0) to (-1m, 3m, 1m) is …..
View SolutionAn automobile of mass m accelerates, starting from rest while engine supplied constant power p. Match the following columns (after t sec).
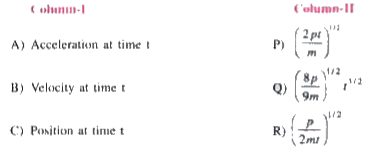
View SolutionAn iron sphere of mass 20×10−3 kg falls through a viscous liquid with terminal velocity 0.5 m/sec. Find the terminal velocity of another iron sphere of mass 54×10−2 kg.
View SolutionIf →A+→B=→Rand2→A+→B is perpendicular to →B then
View SolutionA particle is projected along a horizontal field whose coefficient of friction varies as μ=A/r2, where r is the distance from the origin in meters and A is a positive constant. The initial distance of the particle is 1m from the origin and its velocity is radially outwards. The minimum initial velocity at this point so the particle never stops is
View SolutionThe potential energy of a particle in a force field is: U = (A)/(r^(2)) - (B)/(r ) ,. Where A and B are positive constants and r is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle is
View SolutionA particle is projected with velocity V0along axis x . The deceleration on the particle is proportional to the square of the distance from the origin i.e., a=ωx2.distance at which the particle stops is
View SolutionThe acceleration of a particle increasing linearly with timer is be. The particle starts from the origin with an initial velocity, The distance travelled by the particle in time will be
View Solutionएक कण x -अक्ष के अनुदिश v0 वेग से प्रक्षेपित किया जाता है। कण का मंदन, मूल बिन्दु से इसकी दूरी के वर्ग के समानुपाती है अर्थात् a=−αx2 किस दूरी पर कण रूक जायेगा
View SolutionA particle is projected on x axis with velocity V. A force is acting on it in opposite direction, which is proportional to square of its position. At what distance from origin the particle will stop (m is mass, k = proportionality constant)
View SolutionThe potential energy of a particle in a force field is
U=Ar2−Br
where A and B are positive constants and r is the distance of particle from the centre of the field. For stable equilibirum, the stable equilibrium , the distance of the particle is
View SolutionA particle is projected from origin x-axis with velocity V0 such that it suffers retardation of magnitude given by Kx3 (where k is a positive constant).The stopping distance of particle is
View Solutionएक कण को क्षैतिज क्षेत्र के अनुदिश प्रक्षेपित किया गया है , जिसका घर्षण गुणांक μ=Ar2 के अनुसार परिवर्तित होता है जहाँ r मूल बिनु से दूरी मीटर में है तथा A एक धनात्मक स्थिरांक है। मूलबिंदु से कण की प्रारम्भिक दूरी मीटर है तथा इसका वेग त्रिज्यीय दिशा में बाहर की ओर है। इस बिंदु पर न्यूनतम वेग क्या है जिससे कण कभी न रुके -
View SolutionThe potential energy of a particle in a force field is:
U=Ar2−Br,. Where A and B are positive
constants and r is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle is
View SolutionA particle is projected along a horizontal field whose coefficient of friction varies as mu=A//r^2 , where r is the distance from the origin in meters and A is a positive constant. The initial distance of the particle is 1m from the origin and its velocity is radially outwards. The minimum initial velocity at this point so the particle never stops is
View Solution
