The potential energy for field →F is givenn by U(x,y)=sin(x+y). Find the force acting on the paticle of mass m at a position given by co-ordinates (0,π4). (consider all values in S.I. system)Solution in Telugu
The correct Answer is:1
Step by step video, text & image solution for The potential energy for field vecF is givenn by U(x,y)=sin(x+y). Find the force acting on the paticle of mass m at a position given by co-ordinates (0,(pi)/4). (consider all values in S.I. system) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - PRACTICE SHEET (ADVANCED) (STRAIGHT OBJECTIVE TYPE QUESTIONS)36videos
WORK -POWER-ENERGY
- BOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED MATRIX MATCHING TYPE QUESTIONS)1videos
WORK -POWER-ENERGY
- BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers3videos
VISCOSITY
- BOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 361videos
WORK POWER ENERGY
Similar Questions
The velocity of a particle of mass 10−2kg is given as →v=(2xˆu+3yˆj+4zˆk) m/sec (where x, y and z are in meter). The amount of work done by applied force in displacing a particle from (1m, 2m, 0) to (-1m, 3m, 1m) is …..
03:29View SolutionAn automobile of mass m accelerates, starting from rest while engine supplied constant power p. Match the following columns (after t sec).
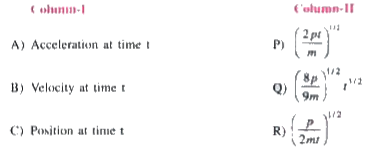 02:36View Solution
02:36View SolutionAn iron sphere of mass 20×10−3 kg falls through a viscous liquid with terminal velocity 0.5 m/sec. Find the terminal velocity of another iron sphere of mass 54×10−2 kg.
02:12View SolutionIf →A+→B=→Rand2→A+→B is perpendicular to →B then
03:58View SolutionThe potential energy of configuration changes in x and y directions as U=kxy , where k is a positive constant. Find the force acting on the particle of the system as the function of x and y.
04:41View SolutionThe potential energy for a force filed →F is given by U(x,y)=cos(x+y). The force acting on a particle at position given by coordinates (0,π/4) is
03:36View SolutionThe potential energy of a force filed →F is given by U(x,y)=sin(x+y). The force acting on the particle of mass m at (0,π4) is
02:58View SolutionFind the expresstion of potential energy U(x,y,z) for a conservative force in a force field where force is given as →F=yzˆi+xyˆk Consider the zero of the potential energy chosen at the point (2,2,2).
01:34View SolutionIf the sum of all value of x satisfying the system of equations
tanx+tany+tanx⋅tany=5
sin(x+y)=4cosx⋅cosy
is kπ2 , where x∈(0,π2) then find the values of k .04:25View SolutionThe potnetial energy for a force field →F is given by U(x,y)=cos(x+y). The force acting on a particle at the position given by coordinates (0,π/4) is
04:45View SolutionThe potential energy U of a body of mass m is given by U = ax + by where x and y are the position coordinates of the particle, the net force acting on the particle is:
01:10View SolutionThe potential energy of a conservative system is given by U=ay2-by,where y represents the position of the particle and a as well b are constants.What is the force acting on the system?
01:54View SolutionThe potential energy of a body of mass m is given by U=ax+by where x,y are position co-ordinate of the particle. The acceleration of the particle is
02:39View SolutionIf the sum of all value of x satisfying the system of equations
tanx+tany+tanx⋅tany=5
sin(x+y)=4cosx⋅cosy
is kπ2 , where x∈(0,π2) then find the values of k .02:12View SolutionThe potential energy of configuration changes in x and y directions as U=kxy , where k is a positive constant. Find the force acting on the particle of the system as the function of x and y.
05:59View Solution

