An ideal spring supports a disc of mass M. A body of mass m is released from a certain height from where it falls to hit M. The two masses stick together at the moment they touch and move together from then on. The oscillations reach to a height a above the original level of the disc and depth b below it. The constant of the force of the spring is

2mgb−a
mgb−a
2mga−b
mg2(a−b)
The correct Answer is:C
Topper's Solved these Questions
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED INTEGER TYPE QUESTIONS)
10 Videos
- VISCOSITY BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers
3 Videos
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 3
61 Videos
Similar Questions
A mass M is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass m dropped from certain height sticks to the mass M after colliding with it.
The oscillations they perform reach to height'a' above the original level of scales & depth 'b' below it.
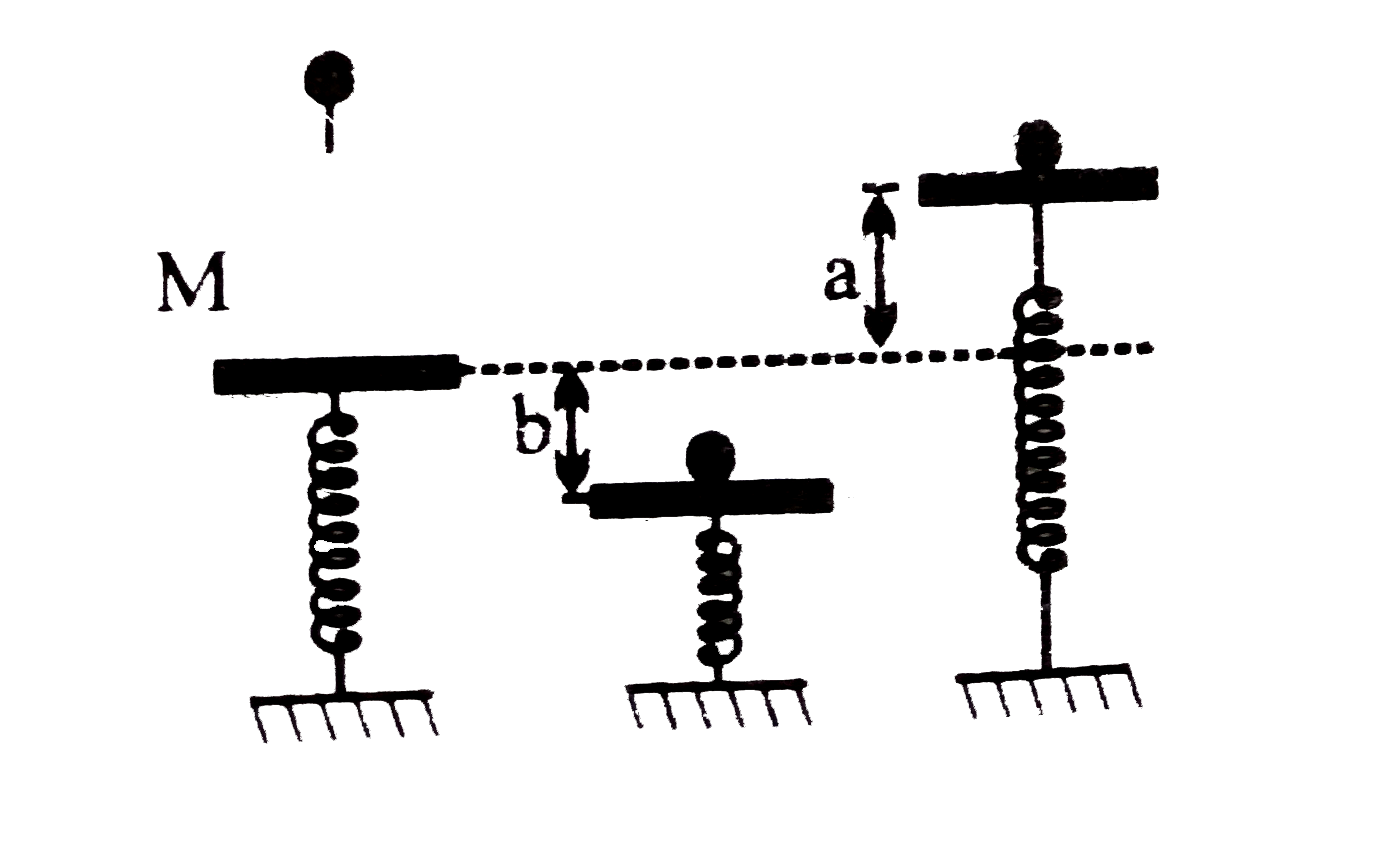
(a) Find the constant of force of the spring.,
(b) Find the oscillation frequency.
(c ) What is the height above the initial level from which the mass m was dropped?
View SolutionA mass M is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass m dropped from certain height sticks to the mass M after colliding with it.
The oscillations they perform reach to height'a' above the original level of scales & depth 'b' below it.
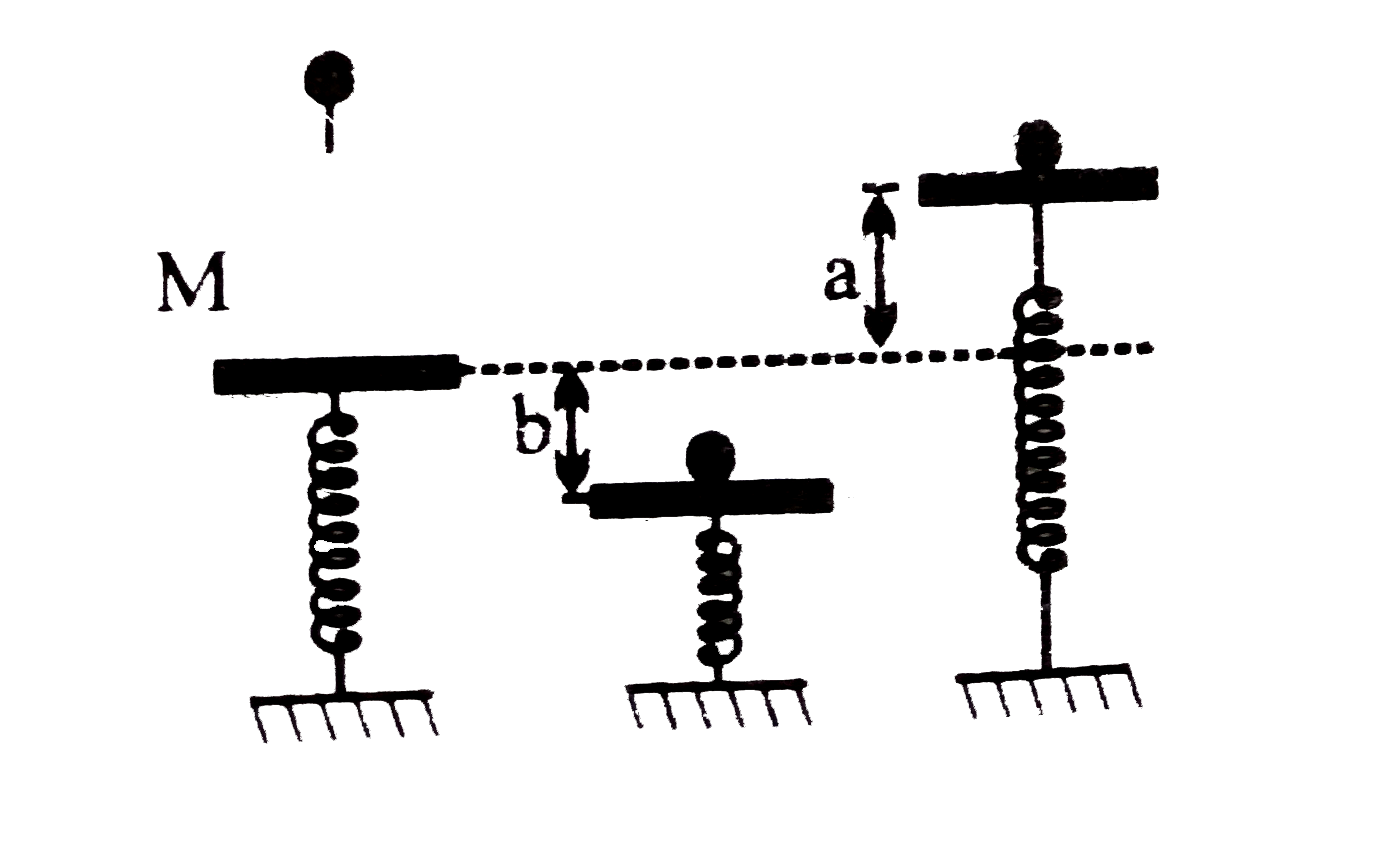
(a) Find the constant of force of the spring.,
(b) Find the oscillation frequency.
(c ) What is the height above the initial level from which the mass m was dropped?
View Solution
Knowledge Check
A body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
Amgk√1−2hkmgBmgkCmgk+mgk√1+2hkmgDmgk−mgk√1−2hkmg
A mass M is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass m dropped from certain height sticks to the mass M after colliding with it.
The oscillations they perform reach to height'a' above the original level of scales & depth 'b' below it.
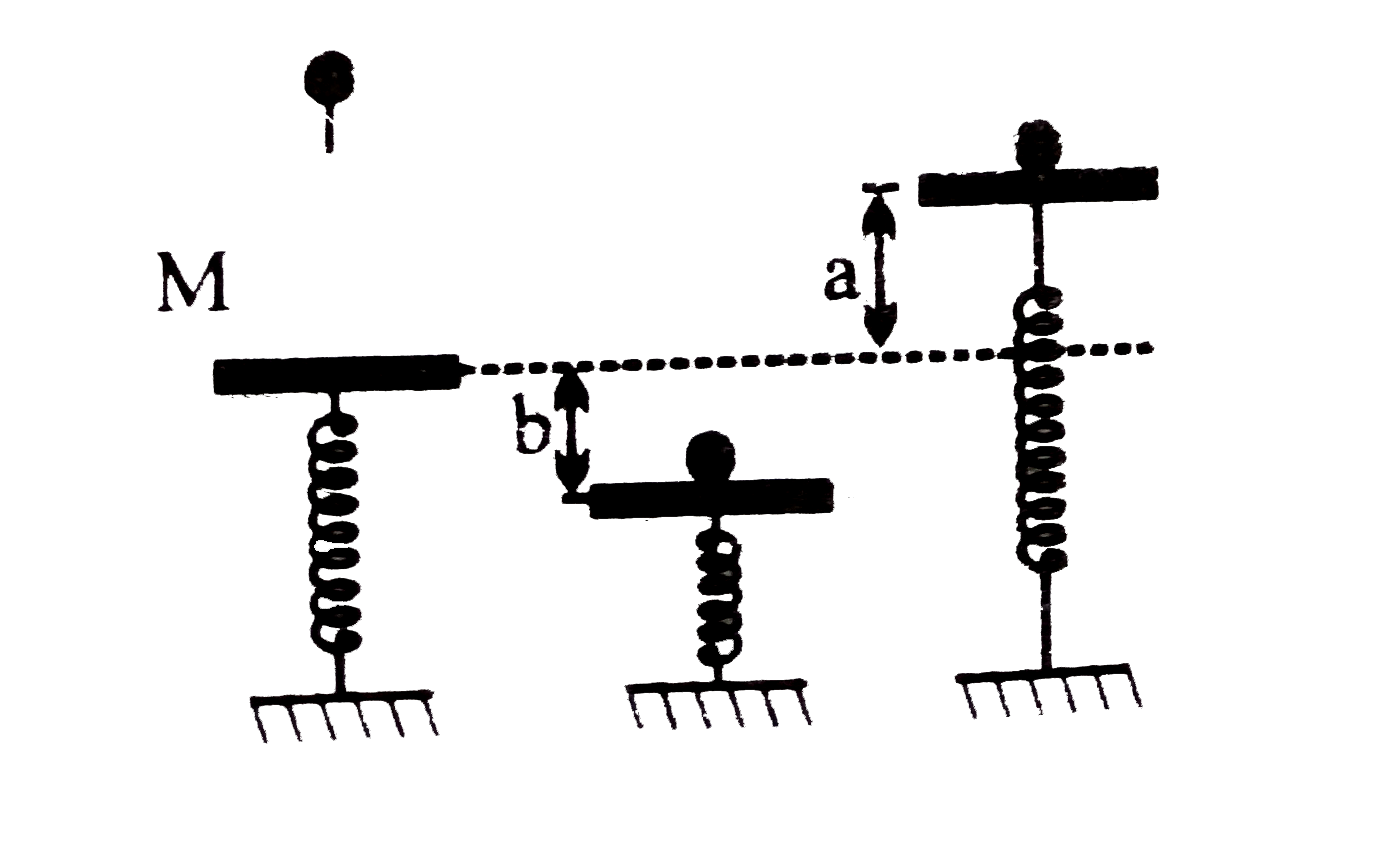
(a) Find the constant of force of the spring.,
(b) Find the oscillation frequency.
(c ) What is the height above the initial level from which the mass m was dropped?
View SolutionA block of mass m is relesed from rest from a height h onto a smooth sledge of mass M fitted with an ideal spring of stiffness k.

View SolutionA body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View SolutionA body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)

View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)

View SolutionA block of mass m is relesed from rest from a height h onto a smooth surface of mass M fitted with an ideal spring of stiffness k. find the maximum compression in the spring.

View Solution
