A copper wire and a steel wire of radii in the ratio 1:2, lengths in the ratio 2:1 are stretched by the same force. If the Young's modulus of copper = 1.1×1011Nm−2 find the ratio of their extensions (young's modulus of steel =2×1011N/m2) .Solution in Telugu
we know e=FLπr2Y⇒e1e2=(L1L2)(r2r1)2(Y2Y1)(FF)
Here , r1:r2=1:2,L1:L2=2:1
Y1=11×1011Nm−2,Y2=2.0×1011Nm−2
e1e2=21(21)2(2.0×10111.1×1011)=161.1=16011
e1:e2=160:11
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE -IA60videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE -IA (MATCHING)4videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-343videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANE EXERCISE - Practice Exercise84videos
MOTION IN A PLANE
Similar Questions
A spring is stretched by applying a load to its free end. The strain produced in the spring is
04:08View SolutionA spring of young's modulus 2×1011 pa is suspended vertically and subjected to a load of 5 kg and elongation is 2 mm. when the load is doubled - match the following (g=9.8m/s2)
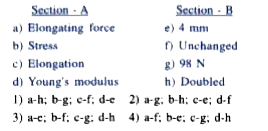 03:20View Solution
03:20View SolutionA U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0cm of water in one arm and 12.5cm of spirit in the other. What is the specific gravity of spirit.
02:08View SolutionA person runs along a circular path of radius 5m. Find the magnitude of the displacement if he runs all the way around the circle ?
02:01View SolutionYoung's modulus of brass and steel are 10×1010N/m and 2×1011N/m2, respectively. A brass wire and a steel wire of the same length are extended by 1mm under the same force. The radii of the brass and steel wires are RB and RS. respectively. Then
03:05View SolutionA steel wire of length 4.7 m and cross-sectional area 3 xx 10^(-6) m^(2) stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4 xx 10^(-6) m^(2) under a given load. The ratio of Young's modulus of steel to that of copper is
03:08View SolutionSteel and copper wires of same length are stretched by the same weight one after the other. Young's modulus of steel and copper are 2xx10^(11)(N)/(m^2) and 1.2xx10^(11)(N)/(m^2) . The ratio of increase in length is
02:19View SolutionA steel wire of length 4.87 mm and cross-section 3.0 xx 10^(-5) m^(2) stretches by the same amout as a copper wire of length 3.5 m and cross -section 4.0 xx 10^(-5) m^(2) under a given load . White is the ratio of the Young's modulus of steel so that of copper ?
03:58View SolutionA steel wire of length 4.5 m and cross-sectional area 3×10−5m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 1×10−5m2 under a given load. The ratio of the Young's modulus of steel to that of copper is
02:57View SolutionThe Young's modulus of brass and steel are respectively 1.0×1011Nm−2 and 2.0×1011Nm−2. A brass wire and a steel wire of the same length are extended by 1 mm each under the same force. If radii of bras and steel wires are RB and Rs respectively, then
View SolutionThe area of cross-section of steel wire is 0.1 cm^(2) and Young's modulus of steel is 2 times 10^(11)N" "m^(-1) . The force required to stretched by 0.1% of its length is
View SolutionA steel wire of length 4.7 m and cross-sectional area 3 xx 10^(-6) m^(2) stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4 xx 10^(-6) m^(2) under a given load. The ratio of Young's modulus of steel to that of copper is
View SolutionA steel wire of length 4.7 m and cross-sectional area 3.0×10−5m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0×10−5m2 under a given load. What is the ratio of the Young's modulus of steel to that of copper ?
05:41View SolutionA steel wire of length 4.6 m and cross section 3×105m2 stretches by the same amount as a copper wire of length 4.0 m and cross section 4.0×10−5m2 under the same load. Find the ratio of the Young.s modulus of steel to that of copper
05:09View SolutionA tension of 22N is applied to a copper wire of cross sectional area 0.02"cm"^(2) , young's modulus of copper is 1.1 xx 10^(11) N//m^(2) and poisson's ratio 0.32. The decrease in cross sectional area will be
03:21View Solution

