A mass .m. is attached with rod as shown in figture. This mass is slightly stretched and released then find the time period. (Y is Young.s modulus of rod, A is cross sectional area of rod, .l. is its length). Solution in Telugu
T=2π√mk⇒T=2π√mlAY
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE -IA60videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE -IA (MATCHING)4videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-343videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANE EXERCISE - Practice Exercise84videos
MOTION IN A PLANE
Similar Questions
A spring is stretched by applying a load to its free end. The strain produced in the spring is
05:46View SolutionA spring of young's modulus 2×1011 pa is suspended vertically and subjected to a load of 5 kg and elongation is 2 mm. when the load is doubled - match the following (g=9.8m/s2)
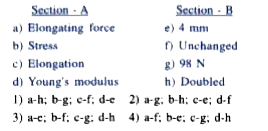02:58View SolutionA U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0cm of water in one arm and 12.5cm of spirit in the other. What is the specific gravity of spirit.
04:10View SolutionA person runs along a circular path of radius 5m. Find the magnitude of the displacement if he runs all the way around the circle ?
04:06View SolutionA mass 'm' is attached with rods as shown in Fig. This mass is slightly stretched and released. Find out whether the motion of mass is S.H.M . If yes then find out the time period.
03:12View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram Ratio of elongation in section PQ of rod and section QR of rod is
05:24View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram Ratio of elastic potential energy stored in section PQ and section QR of the rod is
05:28View SolutionA uniform rod of length L , has a mass per unit length lambda and area of cross section A . The elongation in the rod is l due to its own weight, if it suspended form the celing of a room. The Young's modulus of the rod is
View SolutionA mass m is attached with rods as shown in figure. This mass is slightly stretched and released whether the motion of mass is S.H.M. if yes then find out the time period.
_S01_009_Q01.png)
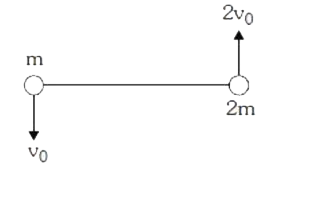
View SolutionTwo point masses of mass m and 2m placed on smooth horizontal plane are connected by a light rod of length l. Masses are given velocities in horizontal plane perpendicular to rod as shown. If area of cross section of rod is A and Young's modulus is Y, then elongation in the rod, will be
02:32View SolutionA uniform rod of mass m and length L is hinged at one of its end with the ceiling and another end of the rod is attached with a thread which is attached with the horizontal ceiling at point P. If one end of the rod is slightly displaced horizontally and perpendicular to the rod and released. If the time period of small oscillation is 2pisqrt((2lsintheta)/(xg)) . Find x.
View SolutionA uniform rod of length Lhasa mass per unit length λ and area of cross-section A. The elongation in the rod is l due to its own weight. If it is suspended from the ceiling of a room, the Young's modulus of the rod is
03:48View SolutionA uniform rod of length Lhasa mass per unit length λ and area of cross-section A. The elongation in the rod is l due to its own weight. If it is suspended from the ceiling of a room, the Young's modulus of the rod is
07:00View SolutionA mass .m. is attached with rod as shown in figture. This mass is slightly stretched and released then find the time period. (Y is Young.s modulus of rod, A is cross sectional area of rod, .l. is its length).
02:41View SolutionA uniform rod of mass m, length L, area of cross-section A and Young.s modulus Y hangs from the ceiling. Its elongation under its own weight will be (MCQ)
01:49View Solution