Given the graph of the function y = f(x) (Fig. 62), find the shape of the graph of the antiderivative I=∫x0f(t)dt
Text Solution
The correct Answer is:x=a2
|
Topper's Solved these Questions
- THE DEFINITE INTEGRAL BOOK - IA MARONCHAPTER - THE DEFINITE INTEGRAL EXERCISE - 6 . 4 (Changing the Variable in a Definite Integral)
30 Videos
- THE DEFINITE INTEGRAL BOOK - IA MARONCHAPTER - THE DEFINITE INTEGRAL EXERCISE - 6. 5 (Simplification of Integrals Based on the Properties of Symmetry of Integrands)
14 Videos
- THE DEFINITE INTEGRAL BOOK - IA MARONCHAPTER - THE DEFINITE INTEGRAL EXERCISE - 6.2 (Evaluating Definite Integrals by the Newton-Leibnitz formula)
17 Videos
- INTRODUCTION OF MATHEMATICAL ANALYSISBOOK - IA MARONCHAPTER - INTRODUCTION OF MATHEMATICAL ANALYSISEXERCISE - Additional Problems
34 Videos
Similar Questions
Knowledge Check
If the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) isA B
B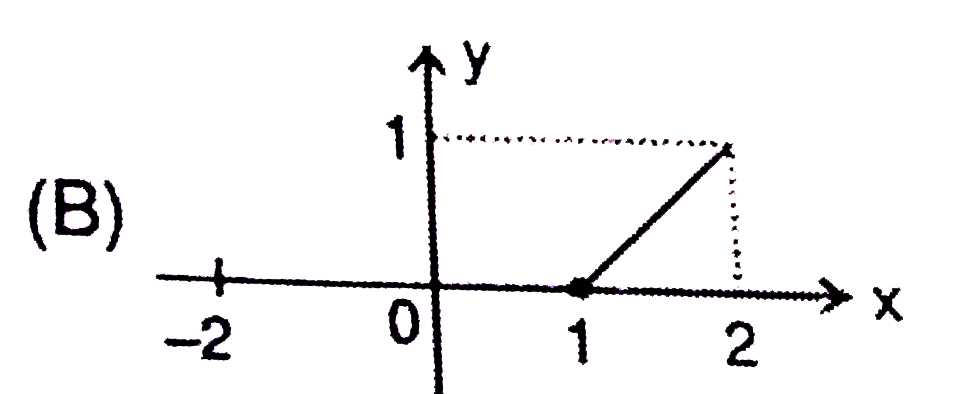 C
C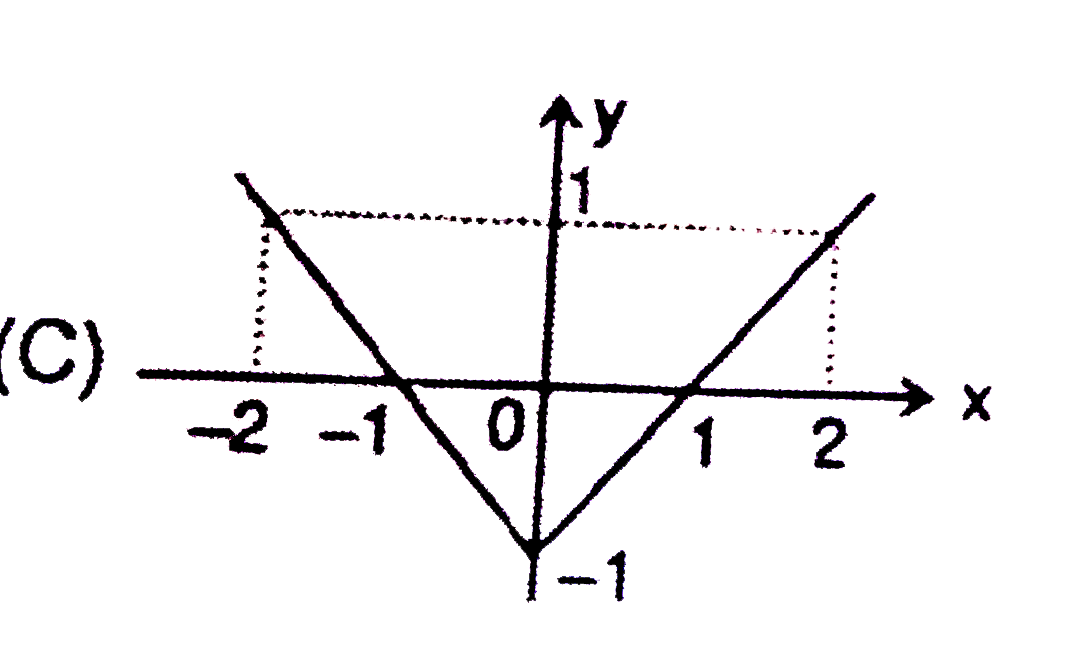 D
D
The graph of y=f(x) is given below
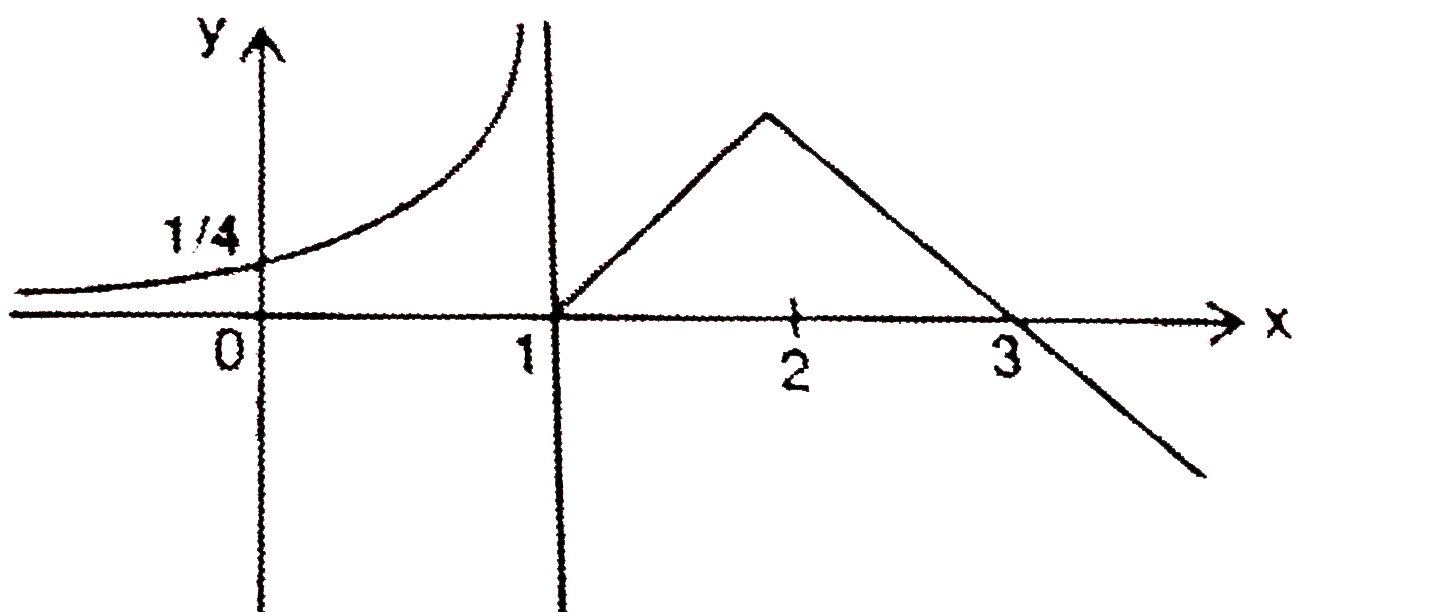
then the graph y=|f(|x|)| is :A B
B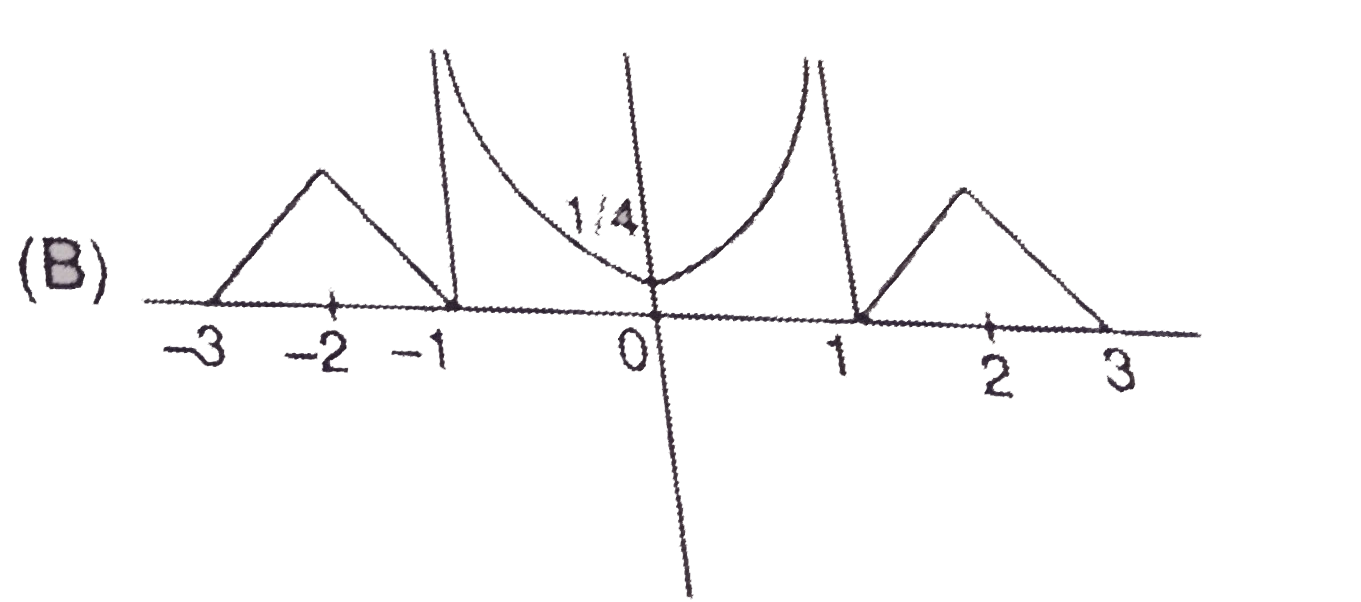 C
C Dnone of these
Dnone of these
If the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) is
View SolutionIf the graph of the function y=f(x) is as shown :

the graph of y=12(|f(x)|−f(x)) is
View SolutionThe angle between the tangent lines to the graph of the function f(x)=∫x2(2t−5)dt at the points where the graph cuts the x-axis is
View SolutionThe graph of y=f(x) is given below

then the graph y=|f(|x|)| is :
View SolutionThe graph of the function y = f(x) is as follows.
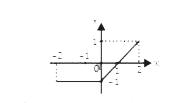
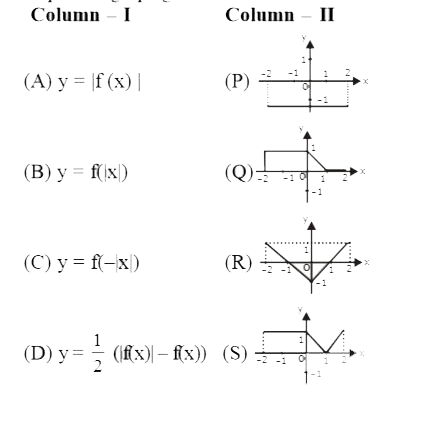
Match the function mentioned in Column-I with the respective graph given in Column-II.
View SolutionLet f be a function such that f(x)>0. Assume that f has derivatives of all orders and that Inf(x)=f(x) ∫x0f(t)dt find f2(0)
View Solution
