Find the average ordinate of the sinusoid over the interval
The correct Answer is:
To find the average ordinate of the sinusoid y=sinx over the interval (0,π), we can use the formula for the average value of a function over an interval (a,b):
Average value=1b−a∫baf(x)dx
In this case, f(x)=sinx, a=0, and b=π.
Step 1: Set up the integral for the average value
We need to calculate:
Average value=1π−0∫π0sinxdx
Step 2: Calculate the integral ∫π0sinxdx
The integral of sinx is:
∫sinxdx=−cosx+C
Thus, we evaluate the definite integral:
∫π0sinxdx=(−cosx)π0
Calculating this gives:
=−cos(π)−(−cos(0))=−(−1)−(−1)=1+1=2
Step 3: Substitute the integral back into the average value formula
Now we substitute the value of the integral back into the average value formula:
Average value=1π⋅2=2π
Conclusion
Thus, the average ordinate of the sinusoid y=sinx over the interval (0,π) is:
2π
---
We need to calculate:
The integral of sinx is:
Now we substitute the value of the integral back into the average value formula:
Thus, the average ordinate of the sinusoid y=sinx over the interval (0,π) is:
Topper's Solved these Questions
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Areas in Rectangular Coordinates
25 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Areas with Parametrically Represented Boundaries
7 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing the Limits of Sums with the Aid
3 Videos
- APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSBOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - ADDITIONAL PROBLEMS
9 Videos
- BASIC CLASSES OF INTEGRABLE FUNCTIONS BOOK - IA MARONCHAPTER - BASIC CLASSES OF INTEGRABLE FUNCTIONS EXERCISE - 5.8 INTEGRATION OF OTHER TRANSCENDENTAL FUNCTIONS
5 Videos
Similar Questions
Knowledge Check
The area enclosed by the curvesy=sinx+cosxandy=|cosx−sinx| over the interval [0,π2]
A4(√2−1)B2√2(√2−1)C2(√2+1)D2√2(√2+1)
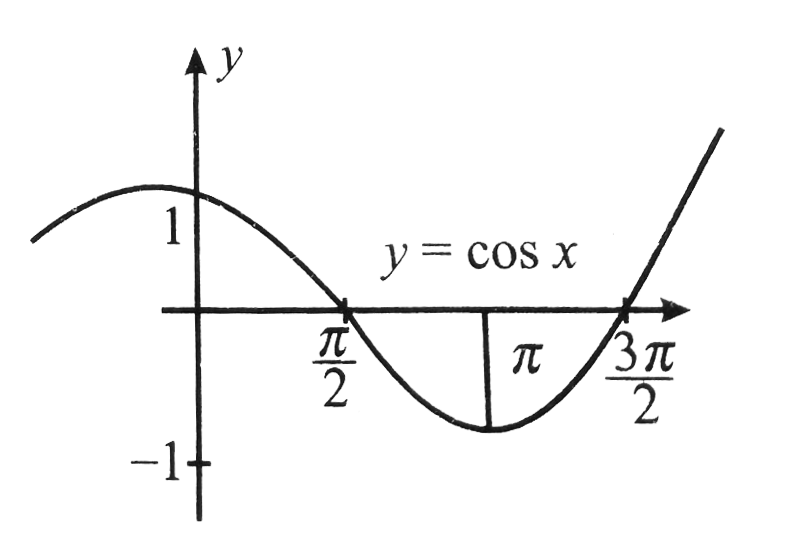
Find the area under the curve y=cosx over the interval
(a) [0,π2]
(b) [0,π]
View SolutionThe area enclosed by the curvesy=sinx+cosxandy=|cosx−sinx| over the interval [0,π2]
View SolutionFind the area bounded by the curve y=x sins-axis in the interval 0≤x≤2π.
View SolutionFind the average value of μ of the function f(x) over the indicated intervals:
(a) f(x)=2x2+1 over [0, 1]
(b) f(x)=1x over [1, 2]
(c ) f(x)=3x−2x+3 over [0, 2]
View SolutionFind the area bounded by the regions y=sinx and the ordinates x=0 and x=2π
View SolutionFind the average values of this functions:
(a) f(x)=sin2x over [0,2π] (b) f(x)=1ex+1 over [0, 2]
View SolutionThe number of solution of the equation |sinx|=|x−1| in the interval [0,π]
View Solution