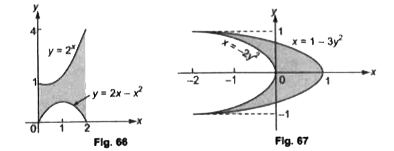
Compute the area of the figure bounded by the straight lines x=0, x=2 and the curves $y = 2^{x}, y = 2 x - x^{2}$

Text Solution

Verified by Experts

The correct Answer is: $- \frac{4}{3}$

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Areas with Parametrically Represented Boundaries
7 Videos
APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - The Area of a Curvilinear Sector in Polar Coordinates
5 Videos
APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Finding Average Values of a Function
15 Videos
APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSBOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - ADDITIONAL PROBLEMS
9 Videos
BASIC CLASSES OF INTEGRABLE FUNCTIONS BOOK - IA MARONCHAPTER - BASIC CLASSES OF INTEGRABLE FUNCTIONS EXERCISE - 5.8 INTEGRATION OF OTHER TRANSCENDENTAL FUNCTIONS
5 Videos

Similar Questions

Knowledge Check

The area of the figure bounded by the curves $y^{2} = 2 x + 1$ and $x - y - 1 = 0$ , is
A $2 / 3$
B $4 / 3$
C $8 / 3$
D $16 / 3$
The area of the region bouned by the curve $y = 2 x - x^{2}$ and the line $y = x$ is
A $1 / 2$
B $1 / 3$
C $1 / 4$
D $1 / 6$

IA MARON-APPLICATIONS OF THE DEFINITE INTEGRAL-Computing Areas in Rectangular Coordinates

Home
Ask Doubt
Profile