Compute the area of the portion of the cylinder surface x2+y2=ax situated inside the sphere
x2+y2+z2=a2
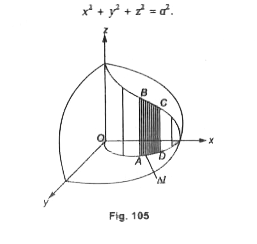
Text Solution
The correct Answer is:4a2
|
Topper's Solved these Questions
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Pressure, Work and Other Physical Quantities by the Definite Integrals
7 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Static Moments and Moments of Inertia. Determining Coordinates of the Centre of Gravity
15 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Area of Surface of Revolution
10 Videos
- APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSBOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - ADDITIONAL PROBLEMS
9 Videos
- BASIC CLASSES OF INTEGRABLE FUNCTIONS BOOK - IA MARONCHAPTER - BASIC CLASSES OF INTEGRABLE FUNCTIONS EXERCISE - 5.8 INTEGRATION OF OTHER TRANSCENDENTAL FUNCTIONS
5 Videos
Similar Questions
Knowledge Check
The area of the portion of the circle x2+y2=1 which lies inside the parabola y2=1−x, is -
Aπ2−23Bπ2+23Cπ2+43Dπ2−43The area of the portion of the circle x2+y2=64 which is exterior to the parabola y2=12x is
A(8π−√3)squnitsB163)(8−√3)squnitsC163)(8π−√3)squnitsDnone of the aboveThe area of the portion of the circle x2+y2=64 which is exterior to the parabola y2=12x is
A(8π−√3)squnitsB163)(8−√3)squnitsC163)(8π−√3)squnitsDnone of the above
The area of the smaller portion of the circle x2+y2=4 cut off the line x+y=2 is
View SolutionThe radius of the sphere x2+y2+z2=12x+4y+3z is
View SolutionThe area of the smaller portion of the circle x2+y2=4 cut off the line x+y=2 is
View SolutionCompute the area of the figure bounded by the parabolas x=−2y2,x=1−3y2
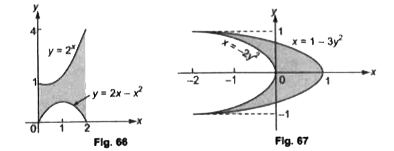
View SolutionWhat is the radius of the sphere x2+y2+z2−x−y−z=0?
View Solution
