The radial distribution function [P(r)] is used to determine the most probable radius, which is used to find the electron in a given orgital $\frac{d P (r)}{d r}$ for 1s-orbital of hydrogen like atom having atomic number Z, is $\frac{d P}{d r} = \frac{4 Z^{3}}{a_{0}^{3}} \frac{2 r - (2 Z r^{2})}{a_{0}} e_{0}^{- 27 x / a_{0}}$ : Then which is the following statements is/are correct ?

A

At the point of maximum value of radial distribution function $\frac{d P (r)}{d r} = 0$ , one anti-node is present

B

Most probable radius of $L i^{2 +}$ is $\frac{a_{0}}{3}$ pm

C

Most probable radius of $H e^{+}$ is $\frac{a_{0}}{2}$

D

Most probable radius of hydrogen atom is (a_0)

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

(a,b,c,d) At the point of maximum value of RDF $\frac{d P}{d r} = 0$
$(2 r - \frac{2 Z r^{2}}{a_{0}}) = 0, r = \frac{a_{0}}{Z}$
Where Z = 3 for $L i^{2 +}$ and Z= 2for the $H e^{+}$ , Z=1 for hydrogen.

|

Updated on:21/07/2023

Class 11 CHEMISTRY STRUCTURE OF ATOM

Similar Questions

Knowledge Check

Question 1 - Select One
The radial distribution functions $[P (r)]$ is used to determine the most probable radius, which is used to find the electron in a given orbital $\frac{d P (r)}{d r}$ for $1 s$ -orbital of hydrogen like atom having atomic number $Z$ , is $\frac{d P}{d r} = \frac{4 Z^{3}}{a_{0}^{3}} (2 r - \frac{2 Z r^{2}}{a_{0}}) e_{0}^{- 2 Z r / a_{0}}$ :
AAt the point maximum value of radial distribution function $\frac{d P (r)}{d r} = 0$ , one antinode is present
BMost probable radius of $L i^{2 +}$ is $\frac{a_{0}}{3}$ pm
CMost probable radius of $H e^{+}$ is $\frac{a_{0}}{2}$ pm
DMost probable radius of hydrogen atom is $a_{0}$ pm
Question 2 - Select One
The plots of radial distribution function for various orbitals of hydrogen atom against 'r' are given below

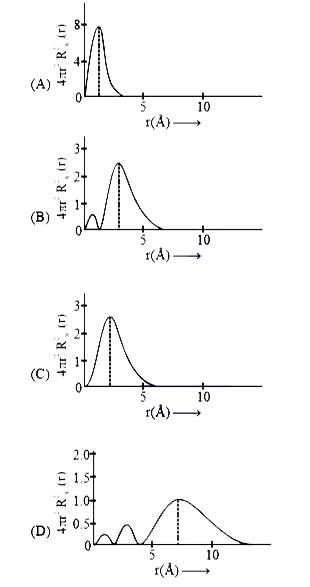
The correct plot for 3s orbital is :
A(B)
B(A)
C(D)
D $(C)$
Question 3 - Select One
From quantisation of angular momentum one gets for hydrogen atom, the radius of the $n^{t} h$ orbit as $r_{n} = (\frac{n^{2}}{m_{e}}) {(\frac{h}{2 π})}^{2} (\frac{4 π^{2} ε_{0}}{e^{2}})$
For a hydrogen like atom of atomic number Z,
Athe radius of the first orbit will be the same
B $r_{n}$ will be greater for larger Z values
C $r_{n}$ will be smaller for larger Z values
Dnone of these

Recommended Questions

Home
Ask Doubt
Profile