A particle in a certain conservative force field has a potential energy given by V=20xyz. The force exerted on it is
(20yz)ˆi+(20xz)ˆj+(20xyz2)ˆk
−(20yz)ˆi−(20xz)ˆj+(20xyz2)ˆk
−(20yz)ˆi−(20xz)ˆj−(20xyz2)ˆk
(20yz)ˆi+(20xz)ˆj−(20xyz2)ˆk
The correct Answer is:B
Topper's Solved these Questions
- WORK POWER ENERGYBook:AAKASH SERIESChapter:WORK POWER ENERGYExercise:EXERCISE - 2
Explore 107 Videos
- WORK -POWER-ENERGYBook:AAKASH SERIESChapter:WORK -POWER-ENERGYExercise:PRACTICE SHEET (ADVANCED) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
Explore 36 Videos
- WORK, POWER & ENERGY Book:AAKASH SERIESChapter:WORK, POWER & ENERGY Exercise:PRACTICE EXERCISE (PERFECTLY INELASTIC COLLISIONS)
Explore 5 Videos
Similar Questions
Knowledge Check
A particle in a certain conservative force field has a potential energy given by U=20xyz. The force exerted on it is
A(20yz)ˆi+(20xz)ˆj+(20xyz2)ˆkB−(20yz)ˆi−(20xz)ˆj+(20xyz2)ˆkC−(20yz)ˆi−(20xz)ˆj−(20xyz2)ˆkD(20yz)ˆi+(20xz)ˆj−(20xyz2)ˆkThe relation between conservative force and potential energy U is given by :–
A→F=dUdxB→F=∫UdxC→F=−dUdxD→F=d2Udx2A particle moves in one dimension in a conservation force field. The potential energy is depicted in the graph below.
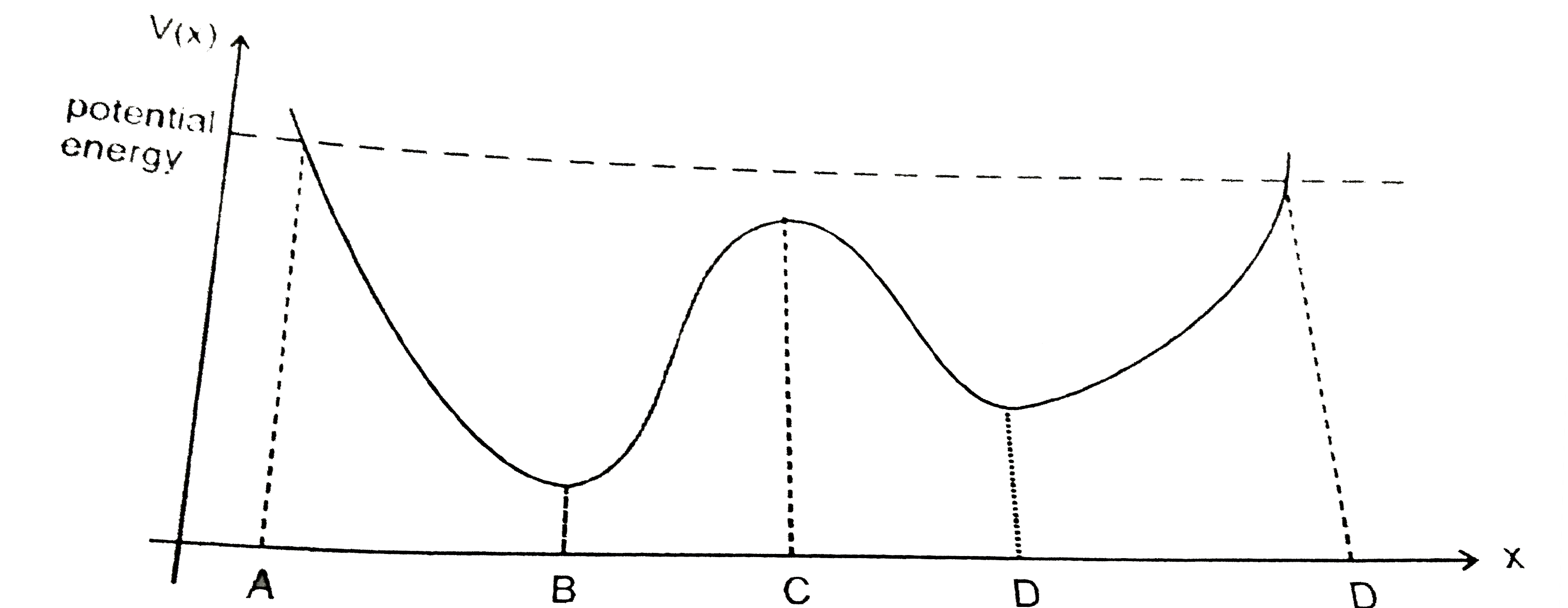
If the particle starts to move from rest from the point A, thenAthe speed is zero at the point A and E.Bthe acceleration vanished at the point A,B,D,C,ECthe acceleration vanished at the points B,C,DDthe speed is maximum at the point D.
A particle moves in one dimension in a conservation force field. The potential energy is depicted in the graph below.

If the particle starts to move from rest from the point A, then
View SolutionA particle is executing simple harmonic motion in a conservative force field. The total energy of simple harmonic motion is given by E=ax2+bv2where ‘x’ is the displacement from mean position x = 0 and v is the velocity of the particle at x then choose the INCORRECT statements.{Potential energy at mean position is assumed to be zero}
View SolutionThe potential energy ‘V’ of a particle moving along the positive x-direction in a conservative force field varies as shown in the figure. The total energy is E=2. Draw the corresponding kinetic energy K vs x graph.
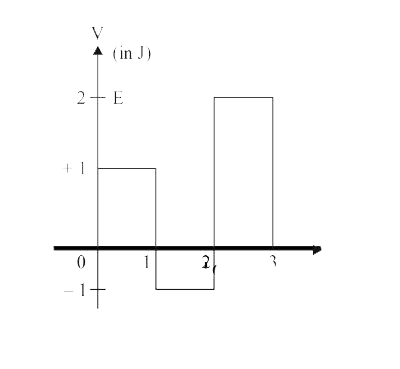
View SolutionThe potential energy ‘V’ of a particle moving along the positive x-direction in a conservative force field varies as shown in the figure. The total energy is E=2. Draw the corresponding kinetic energy K vs x graph.

View SolutionA particle is executing simple harmonic motion in a conservative force field. The total energy of simple harmonic motion is given by E=ax2+bv2where ‘x’ is the displacement from mean position x = 0 and v is the velocity of the particle at x then choose the INCORRECT statements.{Potential energy at mean position is assumed to be zero}
View Solution
