A mass .m. is released, with a horizontal speed v from the top of a smooth and fixed, hemispherical bowl, of radius r. The angle θ w.r.t. the vertical where it leaves constant with the bowl is
sin−1(v23rg+23)
cos−1(v23rg+23)
Tan−1(v23rg+23)
cos−1(2/3)
The correct Answer is:B
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 2107videos
WORK POWER ENERGY
- BOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - PRACTICE SHEET (ADVANCED) (STRAIGHT OBJECTIVE TYPE QUESTIONS)36videos
WORK -POWER-ENERGY
- BOOK - AAKASH SERIESCHAPTER - WORK, POWER & ENERGY EXERCISE - PRACTICE EXERCISE (PERFECTLY INELASTIC COLLISIONS)5videos
WORK, POWER & ENERGY
Similar Questions
A particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.
View Solution
Knowledge Check
- Question 1 - Select One or More
A small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.
AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at B - Question 2 - Select One or More
A small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure. Choose the wrong option (s)
Aacceleration to block is constant throughoutBacceleration of block is g at ACacceleration of block is 3g at BDacceleration of block is 2g at B
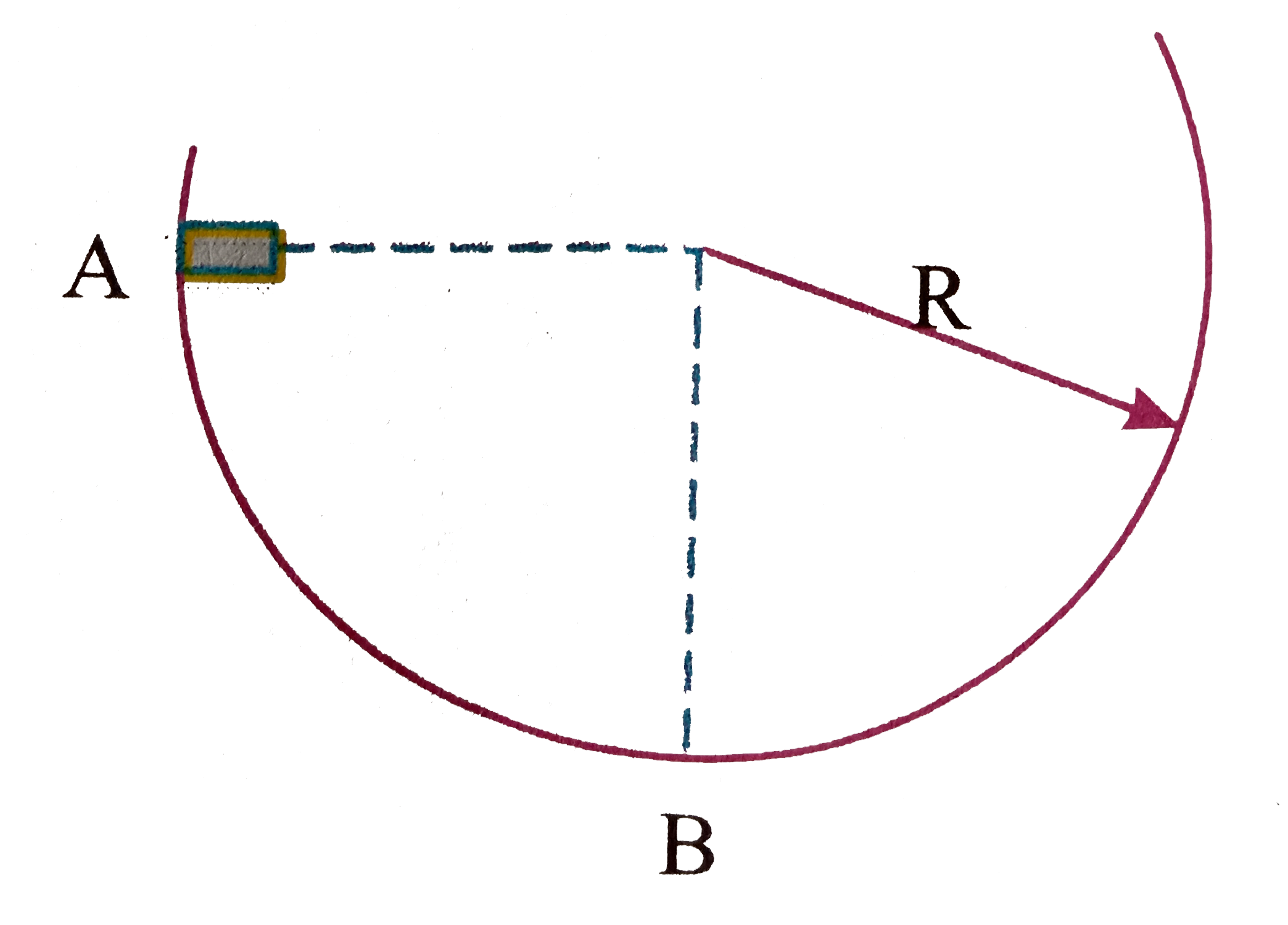
A small mass particle is projected with an initial velocity v0 tangent to the horizontal rim of smooth hemisphereicla bowl at a radius r0 from the vertical centre line, as shown at point A. As the particle slide past point B, a distance h below A and distance r from the verticle centre line, its velocity v makes an angle θ with the horizontal tangent to the bowl through B. Determine θ.
View SolutionA small mass particle is projected with an initial velocity v0 tangent to the horizontal rim of smooth hemispherical bowl at a radius r0 from the vertical centre line, as shown at point A. As the particle slide past point B, a distance h below A and distance r from the vertical centre line, its velocity v makes an angle θ with the horizontal tangent to the bowl through B. Determine θ.
View SolutionA small block of mass m has speed√gR2 at the top most point of a fixed hemisphere of radius R as shown in figure. The angle θ, when block loses the contact with the hemisphere is
_PHY_E05_149_Q01.png)
View SolutionA particle of mass m is placed in equilibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position θ with the vertical where cosθ=35. if the work done against friction is 2mgR10x, find x.
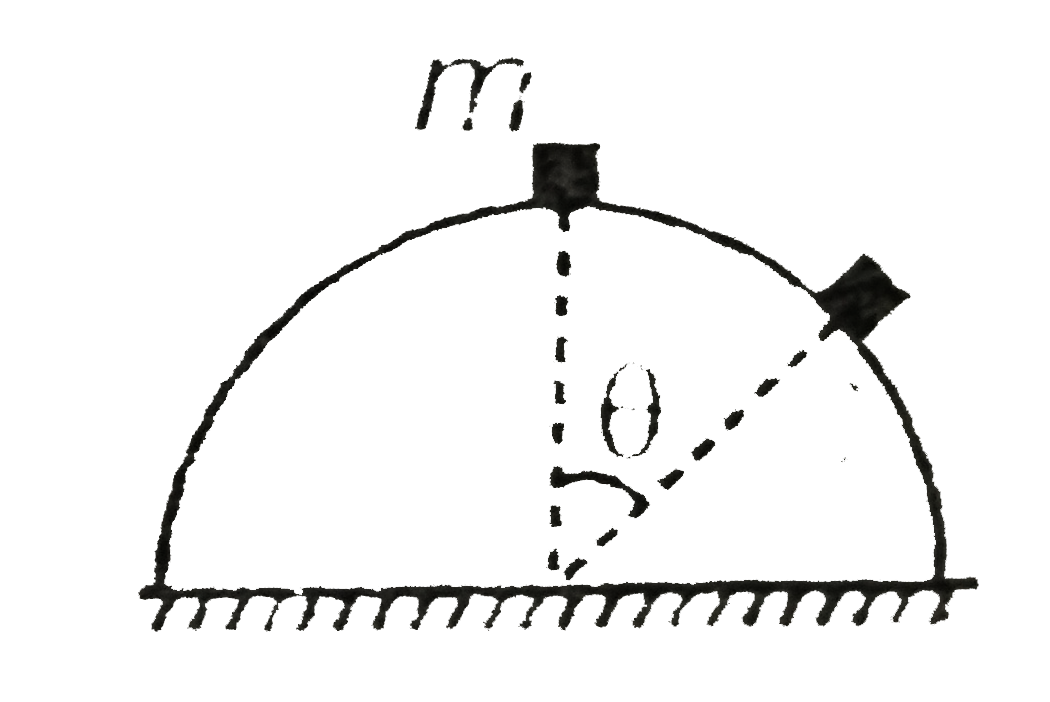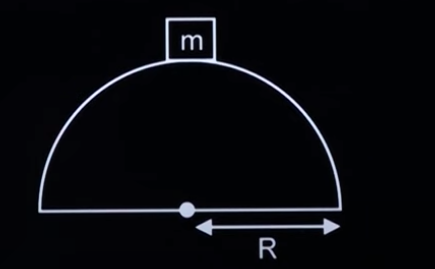
View SolutionA block of mass as shown is released from rest from top of a fixed smooth hemisphere. Find angle made by this particle with vertical at the instant when it looses contact with hemisphere.
View SolutionA small ball is pushed from a height h along a smooth hemispherical bowl of radius R. With what speed should the ball be pushed so that it just reaches the top of the opposite end of the bowl?
View Solution