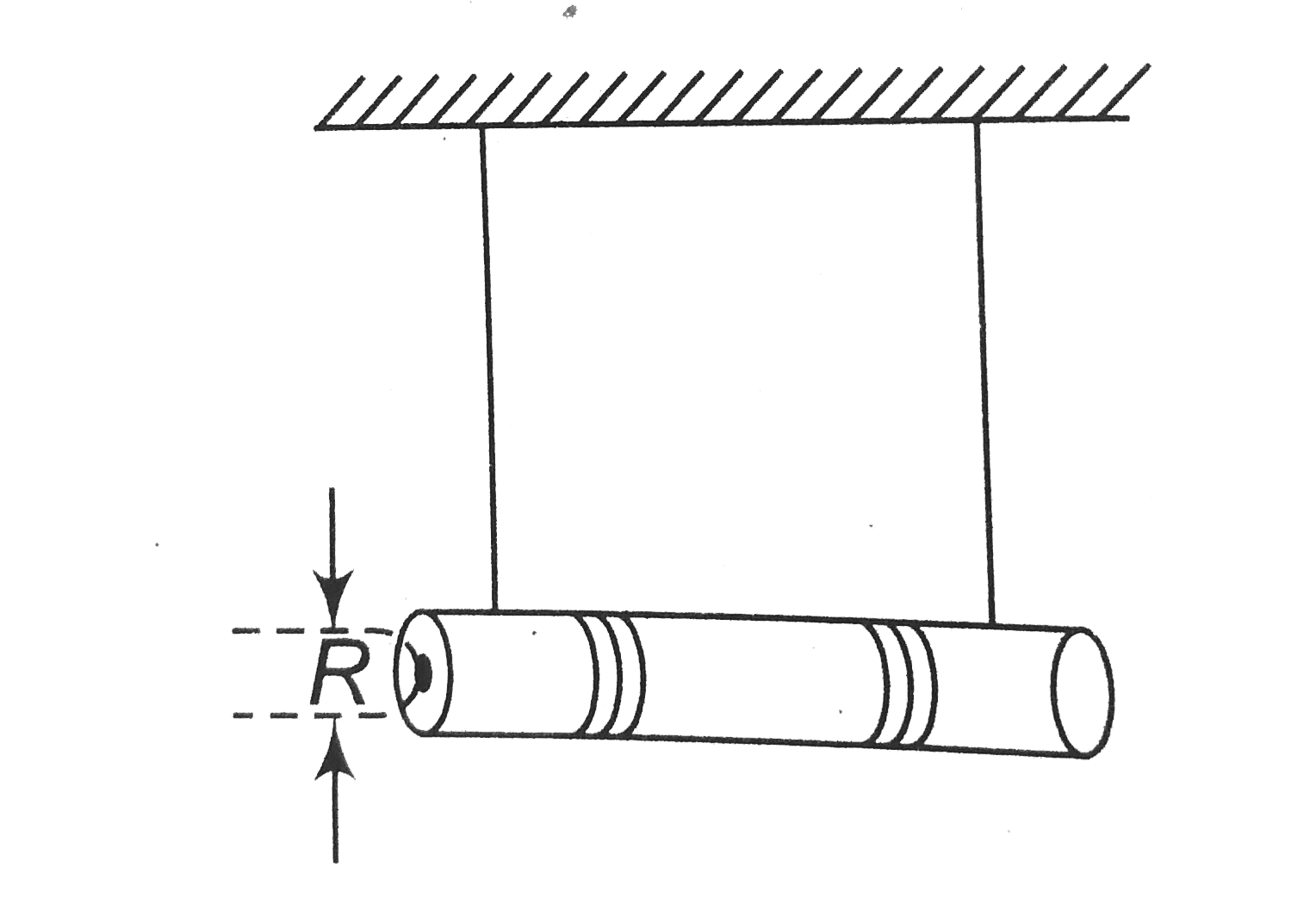
A cylinderical rod of mass .m. length L and radius .R. has two cords wound around it whose ends are attached to a rigid support. The rod is held horizontally with the two cords vertical. When the rod is released, the cords unwind and rod rotates. Find the tension in the cords as they unwound and determine the linear accelerations of the cylinder as it falls.
The rod rotates and translates while falling down.
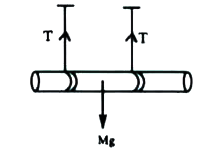
Mg−2T=Ma (translational motion)
2TR=Iα (Rotation motion)
Since I=MR22 and α=aR on solving the above equation we get u=2g3 and T=Mg6
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE - 1A
120 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE - 1B
51 Videos
- SURFACE TENSIONBOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )
8 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
Similar Questions
A cylindrical rod of mass M, length L and radius R has two cords wound around it whose ends are attached to the ceiling. The rod is held horizontally with the two cords vertical. When the rod is released, the cords unwind and the rod rotates the linear acceleration of the cylinder as it falls, is :
 .
.
View SolutionA solid cyinder of mass m=4kg and radius R=10cm has two ropes wrapped around it. one near each end. The cylinder is held horizontally by fixing the two free ends of the cords to the hooks on the ceiling such that both the cords are exactly vertical. The cylinder is released to fall under gravity. Find the linear acceleration of the cylinder.
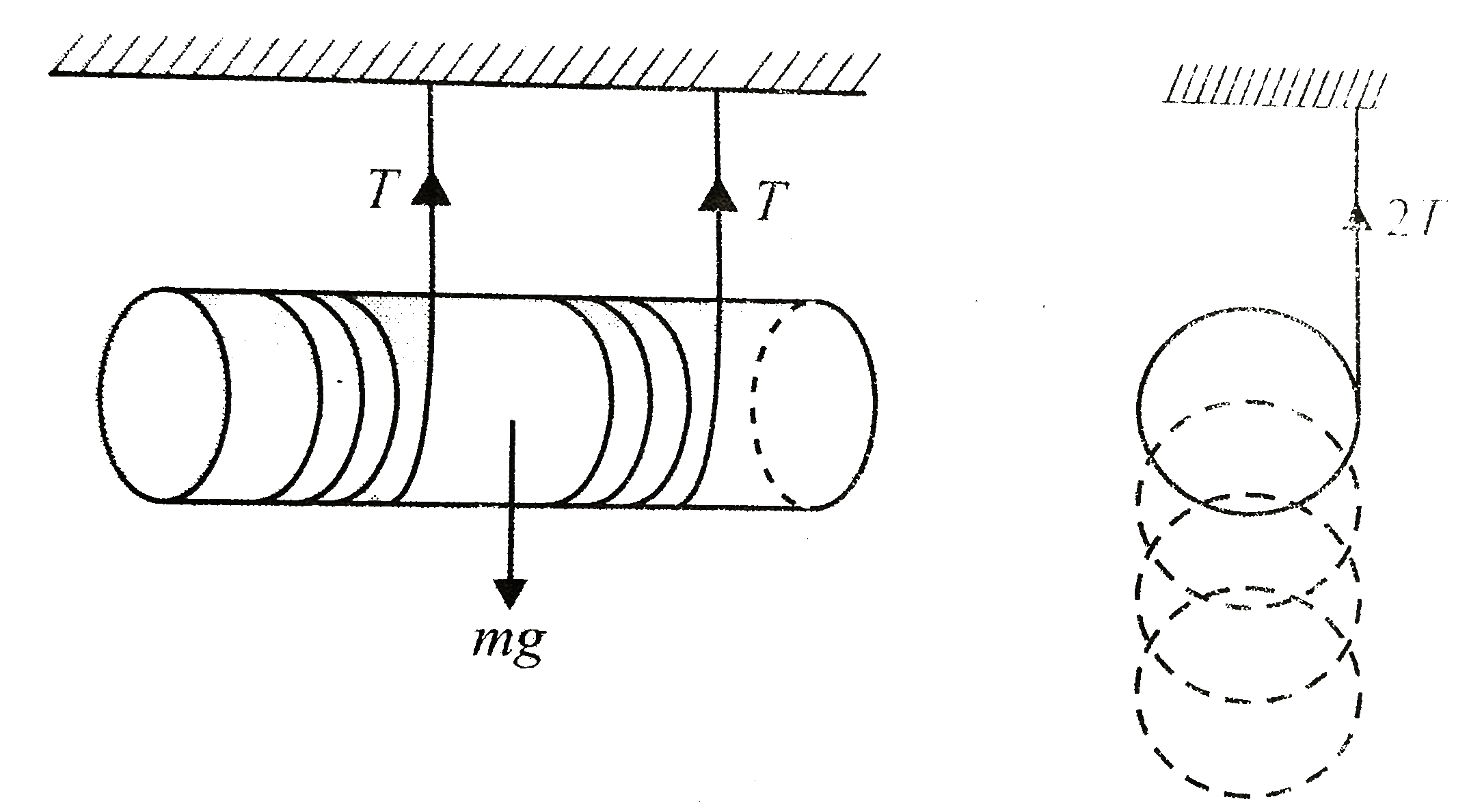
View Solution
Knowledge Check
A cylindrical rod of mass M, length L and radius R has two cords wound around it whose ends are attached to the ceiling. The rod is held horizontally with the two cords vertical. When the rod is released, the cords unwind and the rod rotates the linear acceleration of the cylinder as it falls, is :
 .AgBg3C2g3Dg2
.AgBg3C2g3Dg2A scylindrical rod of mass M, length L & radius R has cords wound around it , whose ends are attached to the ceioling .The rod is held borizontal and released .The liinear acceleration of the cylinder as it falls and tension in the cords is
Ag,Mg/2Bg/3,Mg/3C2g/3,Mg/6Dg/2,Mg/12A solid cylinder of mass m=4kg and radius R=10cm has two ropes wrapped around it, one near each end. The cylinder is held horizontally by fixing the two free ends of he cords to the hooks on the ceiling such that both the cords are exactly vertical. The cylinder is released to fall under gravity. Find the tension along the strings.
A6.53NB5.23NC3.23ND4.43N
A solid cyinder of mass m=4kg and radius R=10cm has two ropes wrapped around it. one near each end. The cylinder is held horizontally by fixing the two free ends of the cords to the hooks on the ceiling such that both the cords are exactly vertical. The cylinder is released to fall under gravity. Find the linear acceleration of the cylinder.
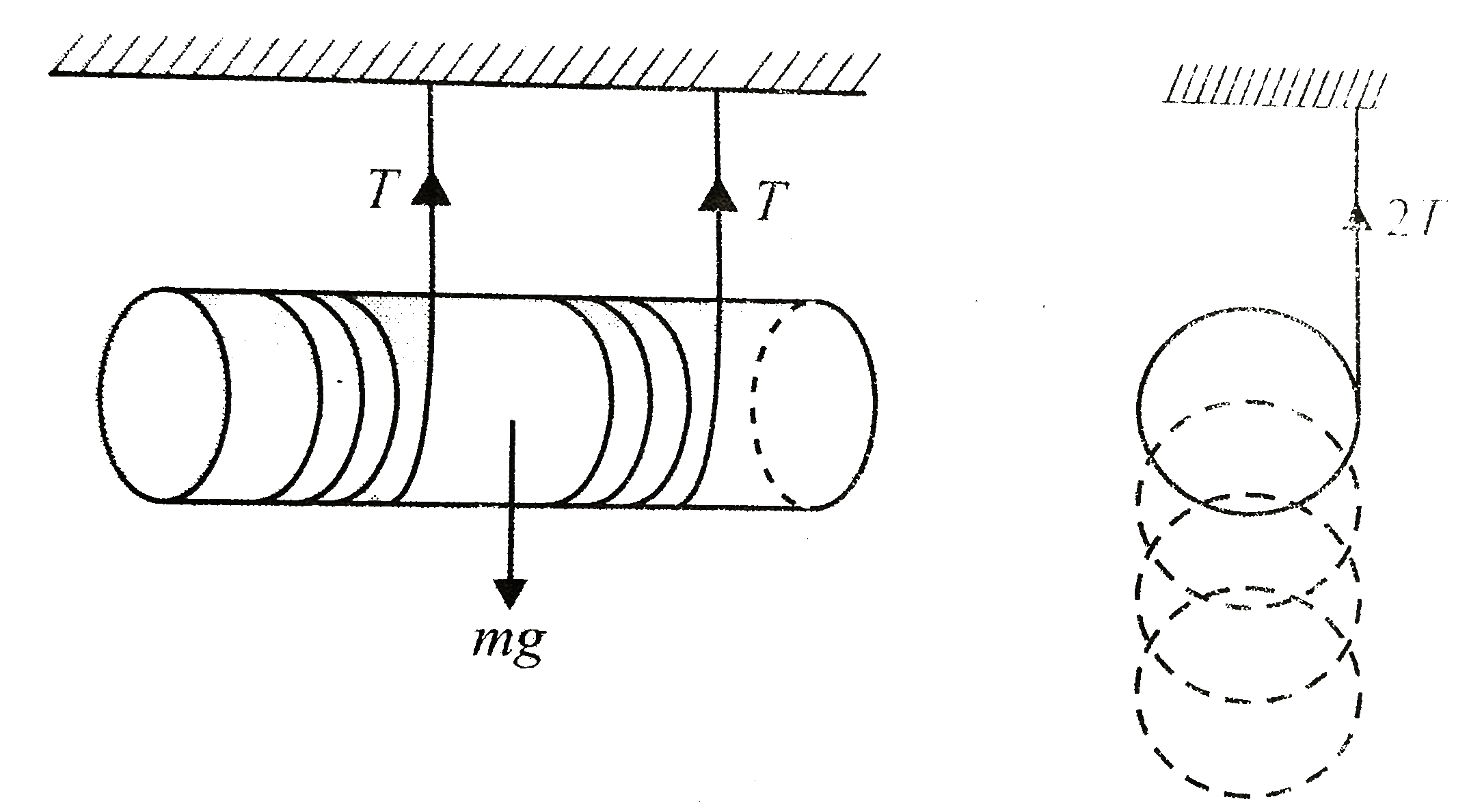
View SolutionA rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View SolutionA small object of mass m, on the end of a light cord, is held horizontally at a distance r from a fixed support as shown. The object is then released. What is the tension in the cord when the object is at the lowest point of its swing?
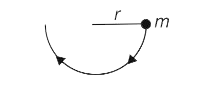
View SolutionOne fourth length of a uniform rod of length 2l and mass m is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.
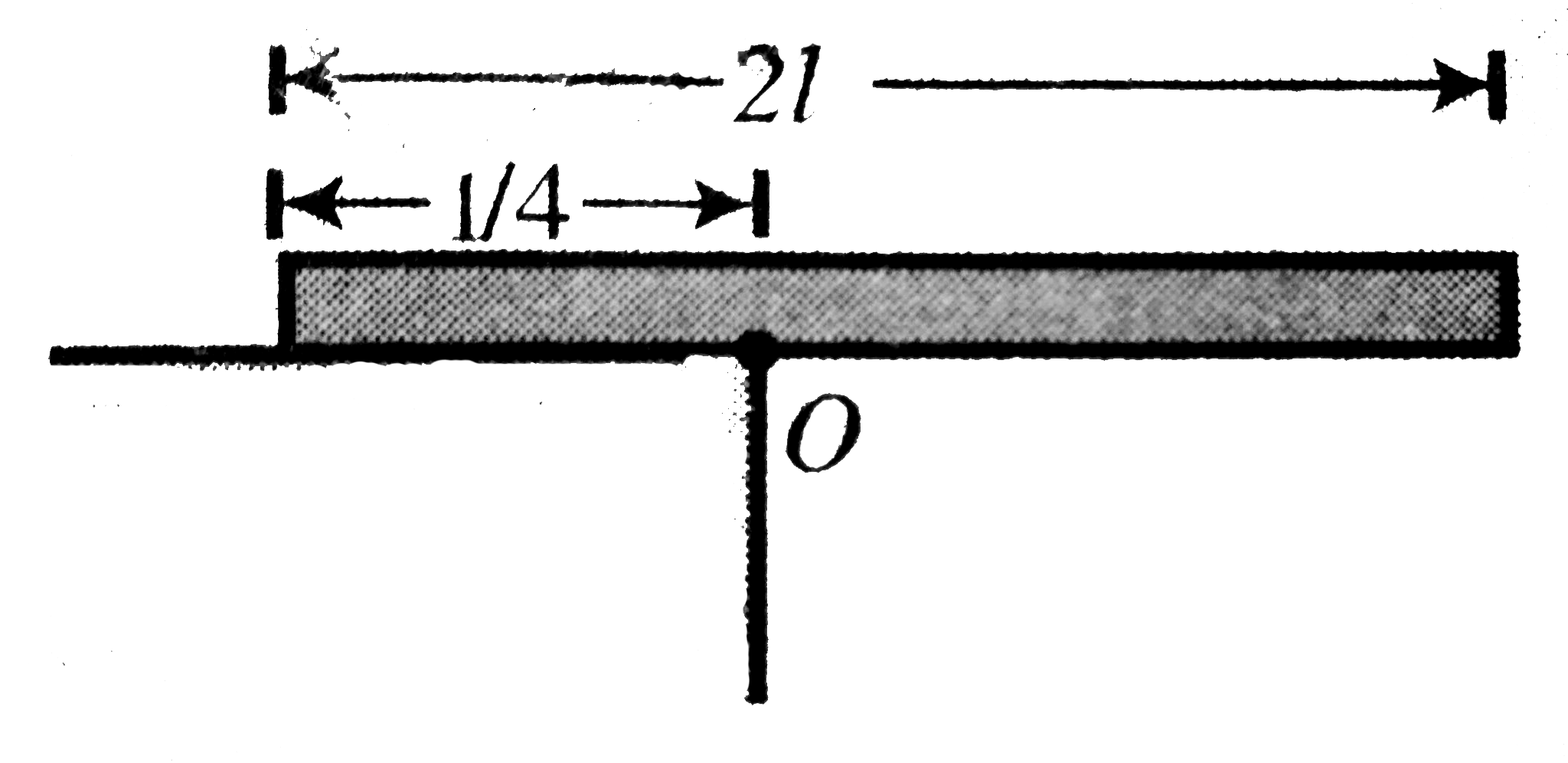
View SolutionA small object of mass m, on the end of a light cord, is held horizontally at a distance r from a fixed support as shown. The object is then released. What is the tension in the cord when the object is at the lowest point of its swing?

View Solution
