A solid cyinder of mass m=4kg and radius R=10cm has two ropes wrapped around it. one near each end. The cylinder is held horizontally by fixing the two free ends of the cords to the hooks on the ceiling such that both the cords are exactly vertical. The cylinder is released to fall under gravity. Find the linear acceleration of the cylinder.
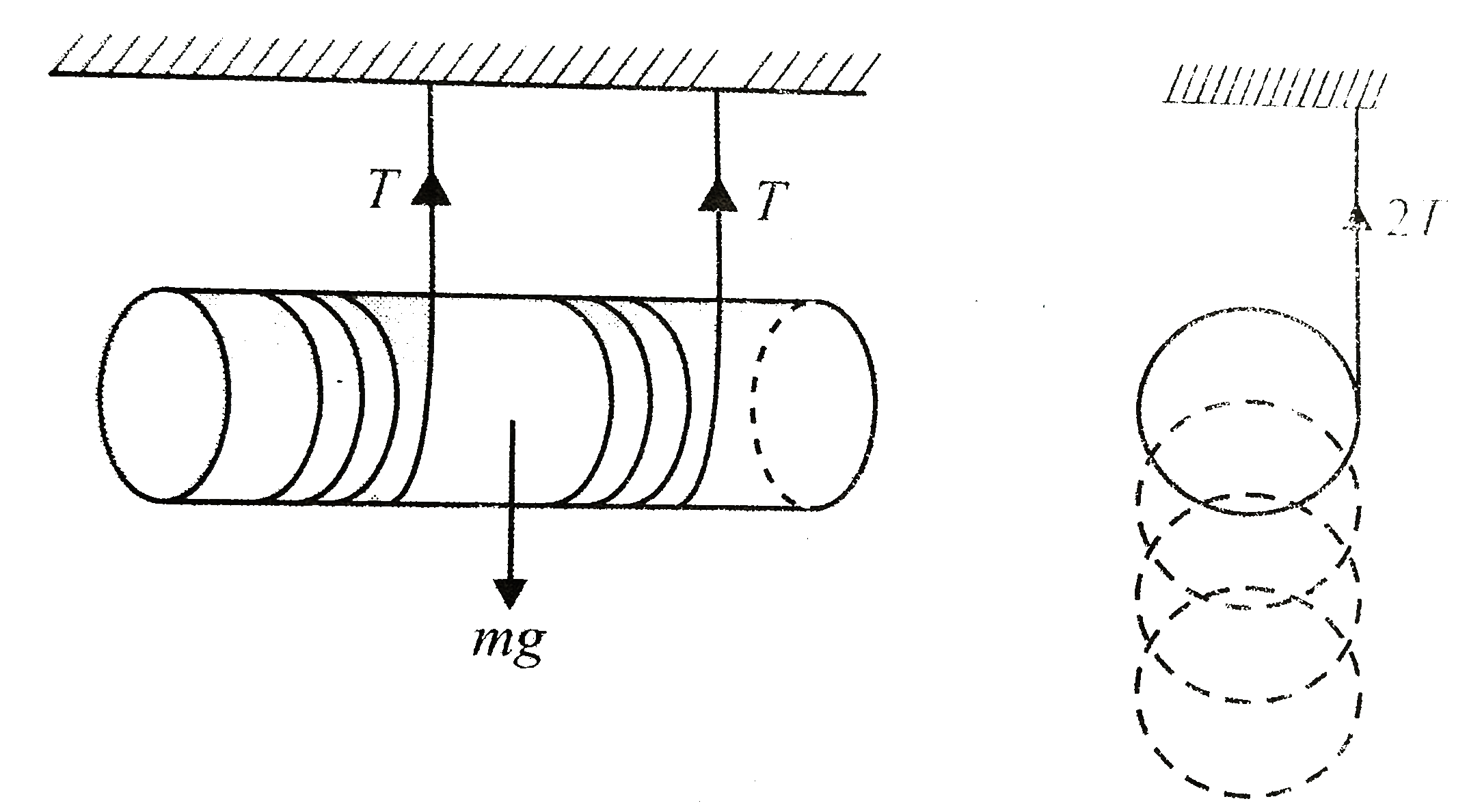
Method 1: Force/Torque Method:
Let a= linear acceleration and α= angular acceleration of the cylinder. For the linear motion of the cylinder.
mg−2T=ma
For the rotational motion: Net torque =Iα

Also, the linear acceleration of the cyinder is the same as the tangential acceleration of an point its surface, a=Rα
Combining the three equations, we get
mg=ma+m2a⇒a=23g
Method 2: Energy method
The motion of the cylinder is rotational and translation combined . Using conservation of mechanical energy
△K=△U=0
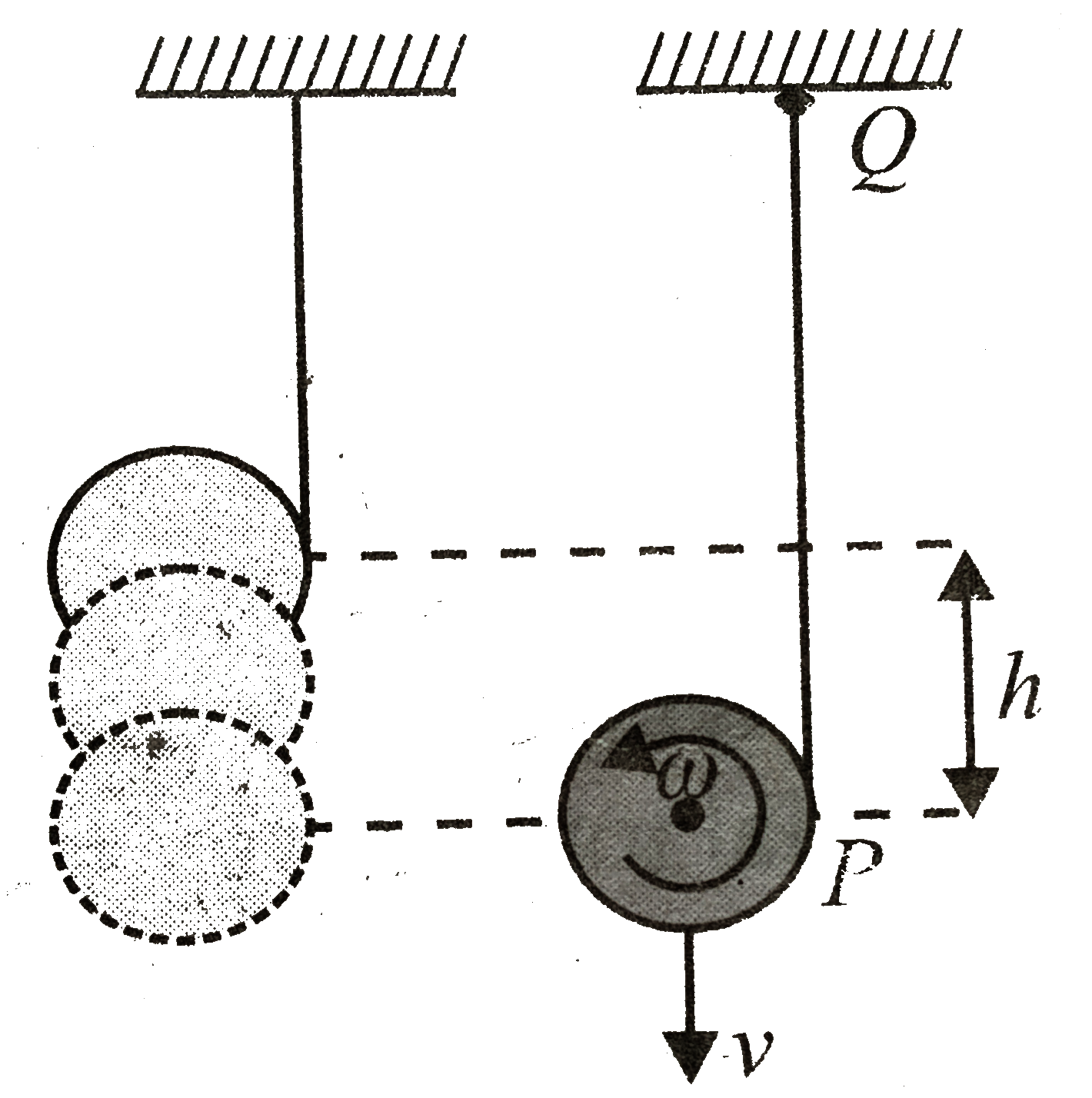
△K+△U=0
or Loss in PE= gain in KE
mgh=12mv2+12Iω2
Constraint relation
Velocity of point PvP=0v−ωR
ω=vR .........i
From eqn and i and ii mgh=12mv2+12(mR2(vR)2
=m2(v2+v22)
2gh=32v2⇒v2=43gh ..... ii
Differentiating eqn iii with respect to time, we get
2vdvdt=43g(dh)dg
22va=43gv⇒a=23g
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
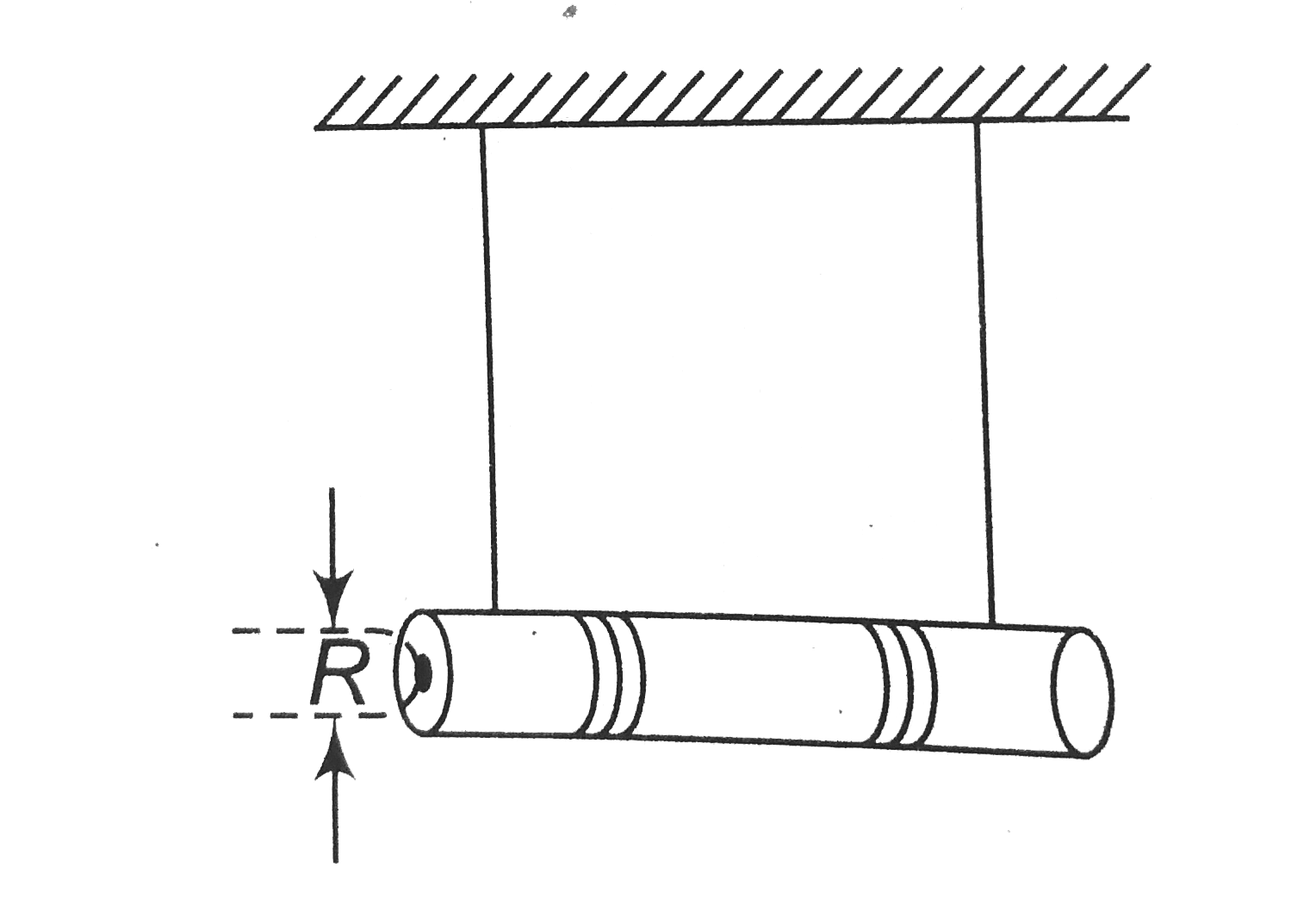
A cylindrical rod of mass M, length L and radius R has two cords wound around it whose ends are attached to the ceiling. The rod is held horizontally with the two cords vertical. When the rod is released, the cords unwind and the rod rotates the linear acceleration of the cylinder as it falls, is :
 .
.
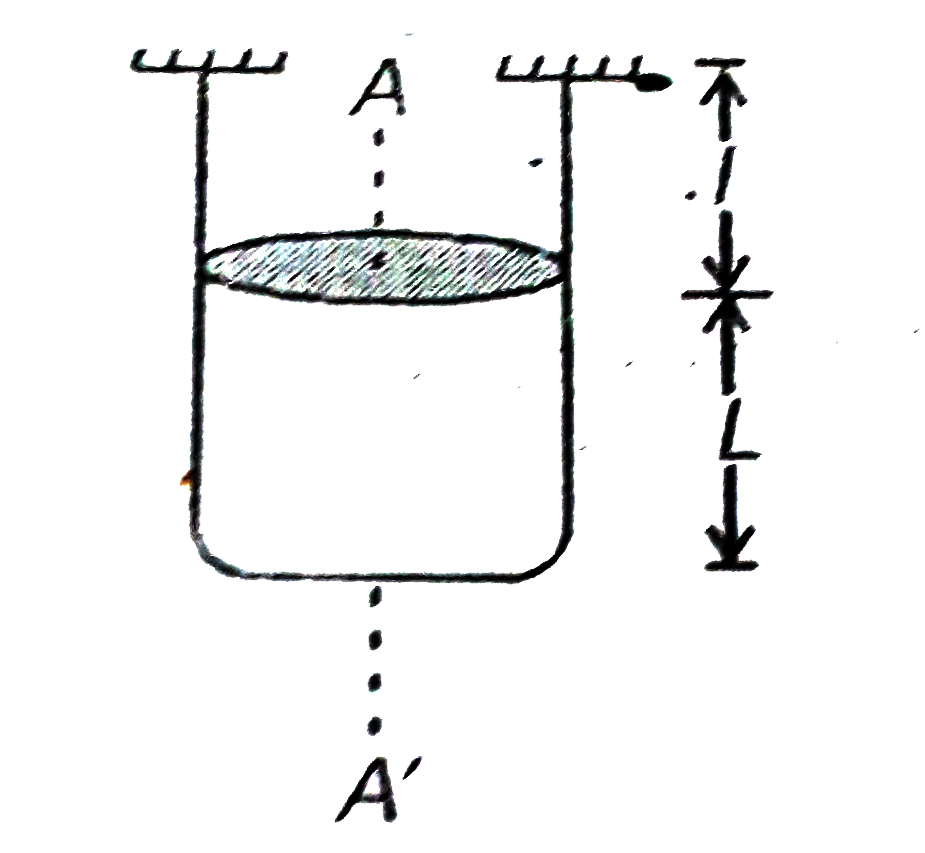
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
View SolutionA plank of mass M, is placed on a smooth surface over which a cylinder of mass m(=M) annd radius R=1m is placed as shown in figure. Now the plane is pulled towards the right wilth an external force F(=2Mg). If the cyinder does not slip over the surfcace of the plank, find the linear acceleration of he plank and the cylinder and the angular acceleration of the cylinder. (Take g=10ms2)

View SolutionOn the surface of a solid cylinder of mass 2 kg and radius 25 cm a string is wound several times and the end of the string is held stationary while the cylinder is released from rest. What is the acceleration of the cylinder and the tension in the string ?
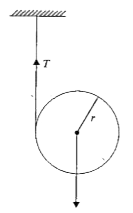
View Solution
A uniform cylider of mass M and radius R has a string wrapped around it. The string is held fixed and the cylinder falls vertically, as in figure.
(a). Show that the acceleration of the cylinder is downward with magnitude a=2g3
(b). Find the tension in the string.
View SolutionA bucket of mass 8 kg is supported by a light rope wound around a solid wooden cylinder of mass 12 kg and radius 20 cm free to rotate about its axis. A man holding the free end of the rope, with the bucket and the cylinder at rest initially, lets go the bucket freely downwards in a well 50 m deep. Neglecting friction, obtain the speed of the bucket and the angular speed of the cylihder just before the bucket enters water.
View SolutionA uniform solid cylinder of mass m and radius 2R rests on a horizontal table. A string attached to it passes over a pulley (disc) of mass m and radius R that is mounted on a fricitonaless axle through its centre . A block of mass m is suspended from the free end of the spring . The string does not slip over the pulley surface and the cylinder rolls without slipping on the table.
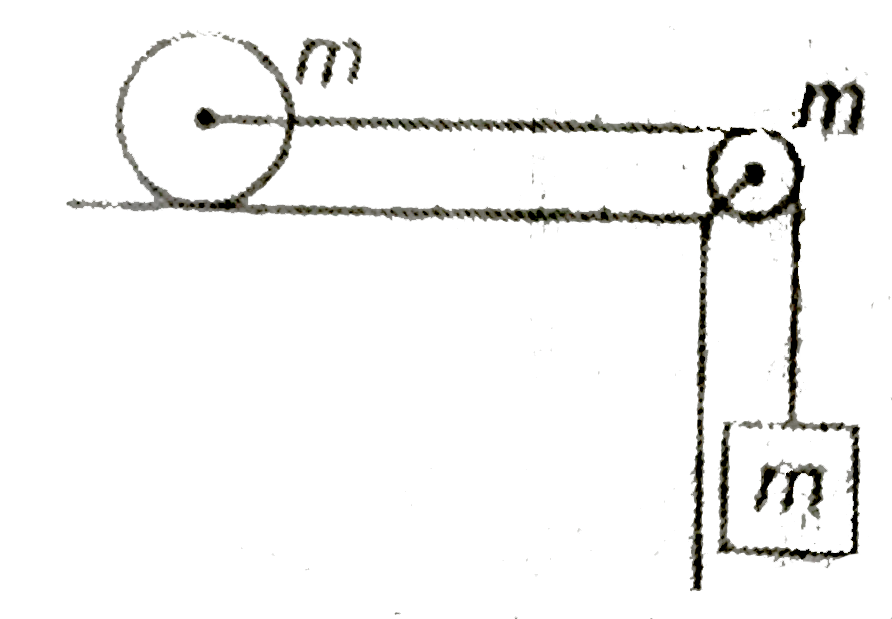
Angular acceleration of the cylinder is
View SolutionA uniform solid cylinder of mass M and of radius R rotates about a frictionless axle. Two masses are suspended from a rope wrapped arround the cylinder. If the system is released from rest, the tension in each rope is?
View Solution
in figure the cylinder of mass 10kg and radius 10 cm has a tape wrapped round it. The pully weighs 100 N and has a radius 5 cm. When the system is released the 5 kg mass comes down and the cylinder rolls without slipping. Calculate the acceleration and velocity of the mass as a function of time.
View SolutionA uniform solid. cylinder A of mass can freely rotate about a horizontal axis fixed to a mount of mass m2. A constant horizontal force F is applied to the end K of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find the acceleration of the point K.
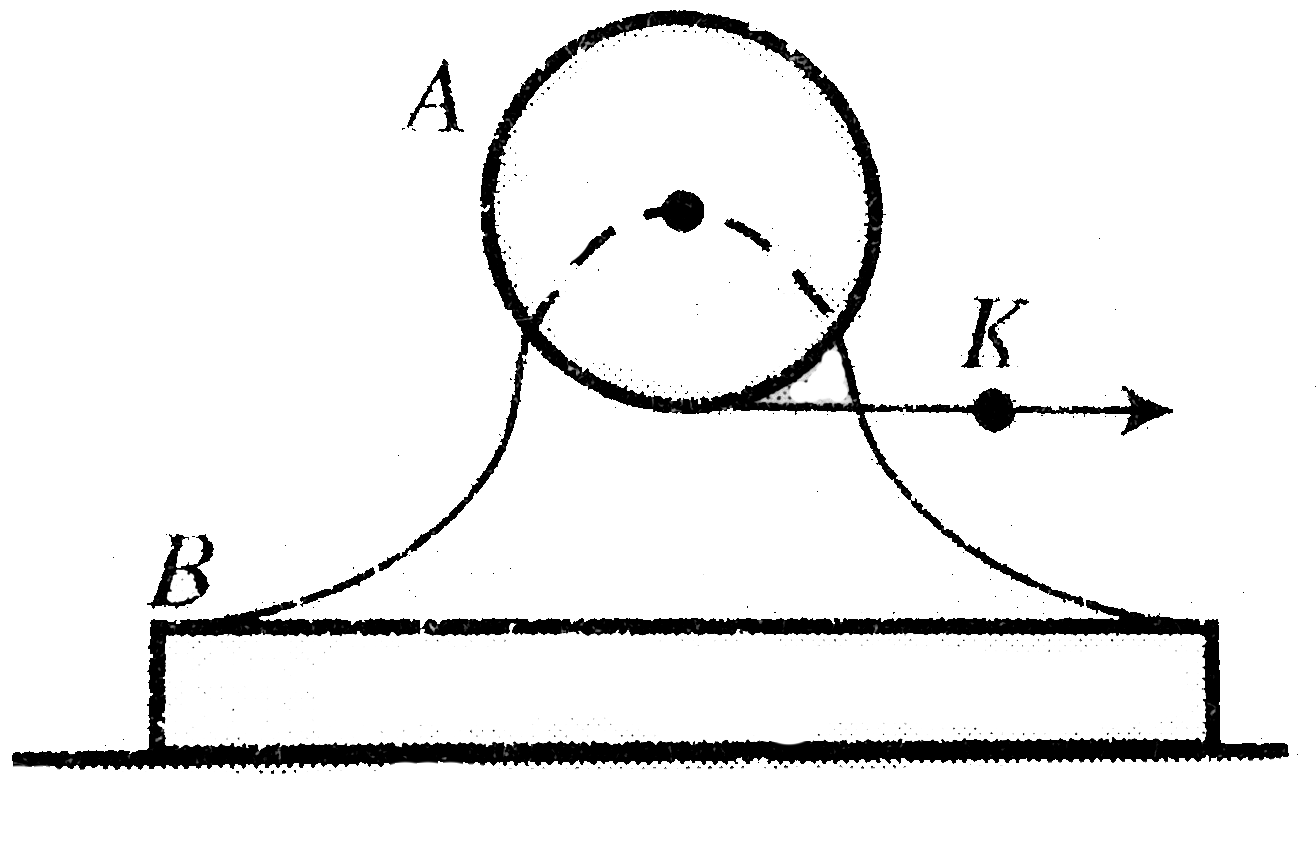
View Solution
