If a simple pendulum has significant amplitude (up to a factor of 1/e of original) only in the period between t = 0 s to 1 = T sec, then T may be called the average life of the pendulum. When the spherical bob of the pendulum of mass 1kg suffers a retardation (due to viscous drag) proportional to into velocity with .b. as the constant of proportionality, the average life time of pendulum is (assuming damping is small) in seconds
b
The correct Answer is:D
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - PROBLEM
249 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE I
184 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE-2
86 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
If a simple pendulum has significant amplitude (up to a factor of 1e of orginal) only in the period between t=0 sec to t=τ sec, then τ may be called the average life of pendulum. When the spherical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity, with 'b' as the constant of proportionality, the average life time of the pendulum is (assuming damping is small) in seconds:
View SolutionIn a simple pendulum the period of oscillation (T) is related to the length of the pendulum (L) as
View Solution
Knowledge Check
If a simple pendulum has significant amplitude (up to a factor of 1/e of original) only in the period between t = Os to t=τs, then τ may be called the average life of the pendulum. When the spherical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity, with 'b' as the constant of proportionality, the average life time of the pendulum is (assuming damping is small) in seconds:
A(a) (0.693)/bB(b) bC(c )1bD(d) 2bA simple pendulum is set into vibrations. The bob of the pendulum comes to rest after some time due t
AAir frictionBMoment of inertiaCweight of the bobDCombination of all the aboveIf T and T' are the periods of a simple pendulum and a conical pendulum of the sample length then .
AT=T'BT<T'CT>T'DT=12T'
If the time period of a pendulum is 1sec, then what is the length of the pendulum at point of intersection of l−T and l−T2 graph.
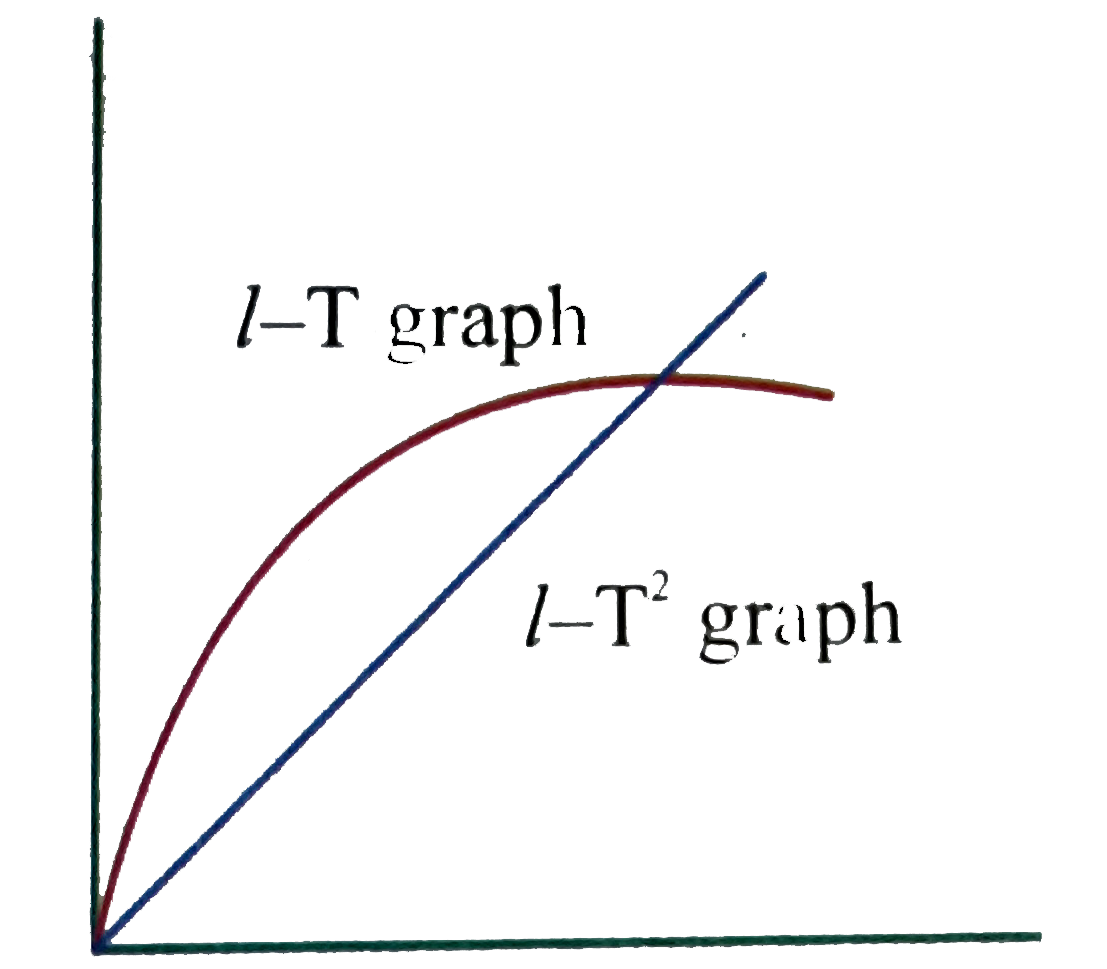
View SolutionIn a simple pendulum the period of oscillation (T) is related to the length of the pendulum (L) as
View SolutionA simple pendulum performs SHM about x=0 an amplitude a and time period T. the speed of pendulum at x=a2 will be
View SolutionA simple pendulum performs simple harmonic motion about x=0 with an amplitude a and time period T speed of the pendulum at x=a/2 will be
View SolutionA simple pendulum has a time period T. The pendulum is completely immersed in a non-viscous liquid whose density is one-tenth of that of the material of the bob. The time period of the pendulum immersed in liquid is
View Solution
