A simple pendulum ia hanging from a per inserted in a vertical wall. Its bob is stretched to horizontal position from wall and is left free to move, the bob hits the wall. If coefficient of restitution is 2√5. After how many collision the amplitude of vibration will become less than 60∘ (Hint : hn≤h(1−cosθ))
6
3
5
4
The correct Answer is:D
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - PROBLEM
249 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE I
184 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE-2
86 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
A simple pendulum is supended from a peg on a verticl wall. The pendulum is pulled away from the wall to a horizontal position and releases as shown in figure −4.152. The ball hits the wall, the coefficient of restitution being 2/√2. What is the minimum number of collisions after which the amplitude of oscillation becomes less than 60∘
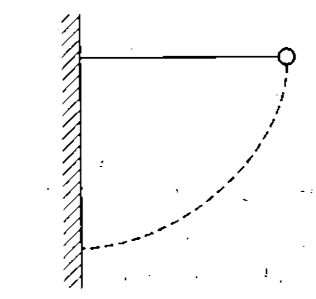
View SolutionA ball is attached to a string of length L. The ball is released when the string is horizontal. The ball collides with wall and e=2/√5. After how many minimum number of collisions , the amplitude of oscillation becomes less than 60∘.

View Solution
Knowledge Check
A simple pendulum is hanging from a peginserted in a vertical wall. Its bob is strteched to horizontal position form wall and left freee to move, the bob hits the wall. If coefficient of restitution is 2√5. After how many collisions the amplitude of vibration will becomes less then 60∘.
A6B3C5D4A simple pendulum is hanging from a peg inserted in a vertical wall. Its bob is stretched in horizontal position from the wall and is left free to move. The bob hits on the wall the coefficient of restitution After how many collsions the amplitude of vibration will become less than 60∘
A6B3C5D4A simple pendulum of length hangs from a horizontal roof as shown in figure. The bob of mass m is given an initial horizontal velocity of magnitude √5gl as shown in figure. The coefficient of restitution e=12. After how many collisions the bob shall no long come into constant with the horizonrtal roof?
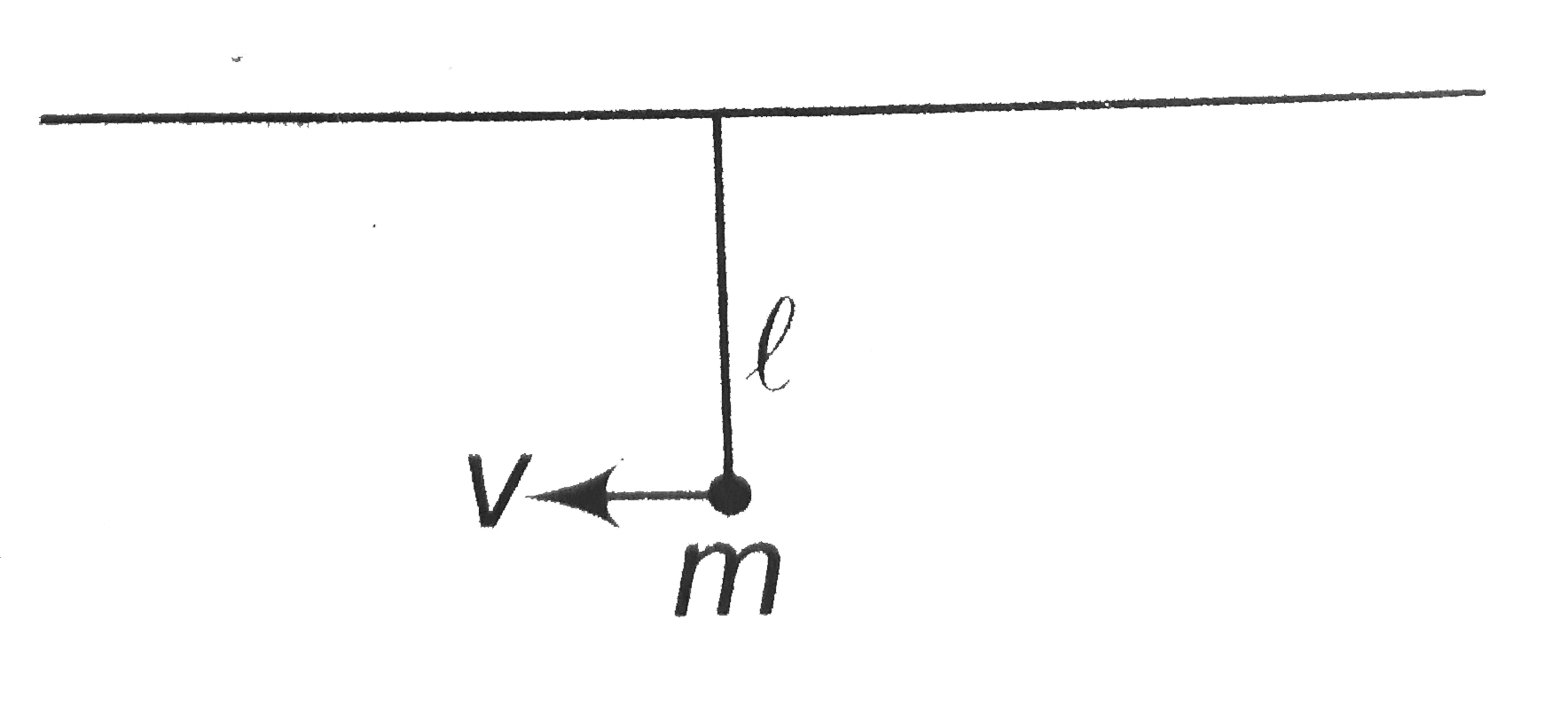 A1B2C4Dnone of these
A1B2C4Dnone of these
A simple pendalum is suspended from a peg on a verticle wall . The pendulum is pulled away from the well is a horizental position (see fig) and released . The bell his the well the coefficient of resitution being 2√5
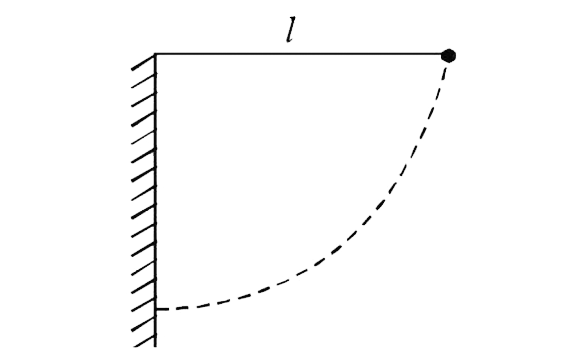
what is the miximum number of colision after which the amplitube of secillections between less that 60 digree ?
View SolutionA simple pendalum is suspended from a peg on a verticle wall . The pendulum is pulled away from the well is a horizental position (see fig) and released . The bell his the well the coefficient of resitution being 2√5
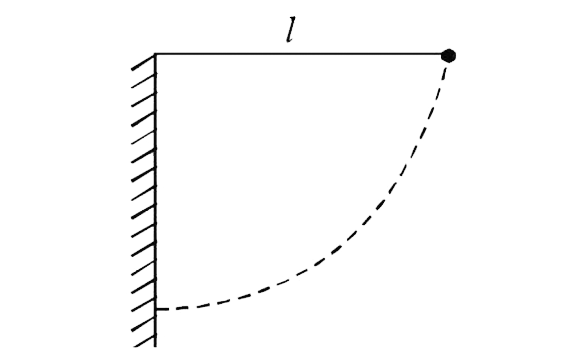
what is the miximum number of colision after which the amplitube of secillections between less that 60 digree ?
View SolutionA simple pendalum is suspended from a peg on a verticle wall . The pendulum is pulled away from the well is a horizental position (see fig) and released . The bell his the well the coefficient of resitution being 2√5
what is the miximum number of colision after which the amplitube of secillections between less that 60 digree ?
View SolutionA simple pendulum is suspended from a peg on a wall which is inclined at an angle of 30∘ with the vertical. The pendulum is pulled away from the wall to a horizontal position (with string just taut) and released. The bob repeatedly bounces off the wall, the coefficient of restitution being e=2√5
Find the number of collisions of the bob with the wall, after which the amplitude of oscillation (meaured from the wall) becomes less than 30∘

View SolutionA small ball is projected from point P towards a vertical wall as shown in Fig. It hits the wall when its velocity is horizontal. Ball reaches point P after one bounce on the floor. The coefficient of restitution assuming it to be same for two collisions is n/2. All surfaces are smooth. Find the value of n.

View Solution
