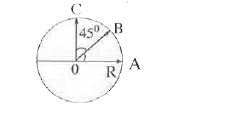
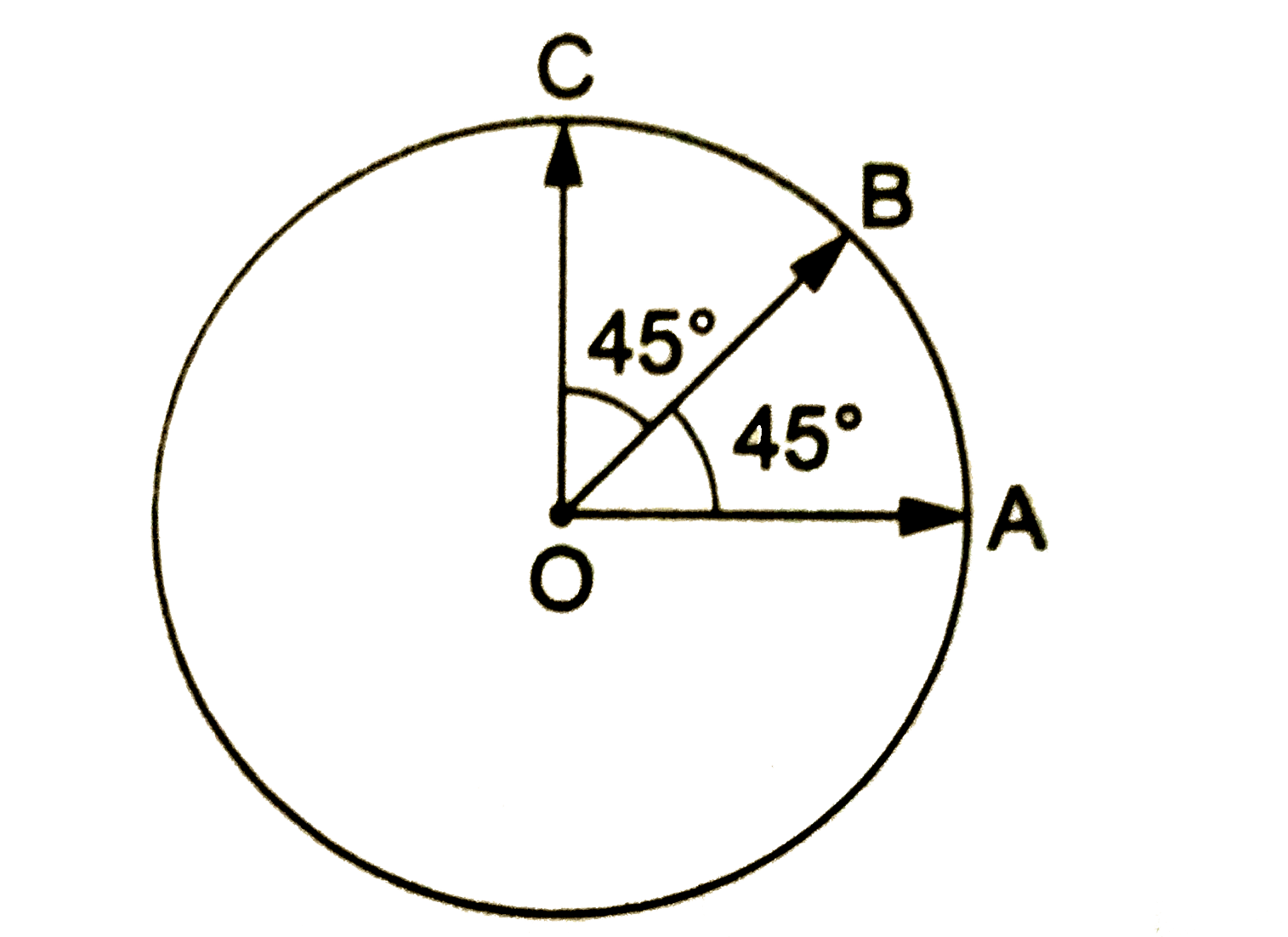
The resultant of the three vectors ¯¯¯¯¯¯OA,¯¯¯¯¯¯OBand¯¯¯¯¯¯OC has magnitude (R = Radius of the circle)
 Solution in Telugu
Solution in Telugu
√2R
(1+√2)R
(√2−1)R
2R
The correct Answer is:B
Step by step video & image solution for The resultant of the three vectors bar(OA), bar(OB) and bar(OC) has magnitude (R = Radius of the circle) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTORSBOOK - AAKASH SERIESCHAPTER - VECTORSEXERCISE - Lecture Sheet (Exercise-I) (Addition of Vectors) (More than correct answer type Questions)
2 Videos
- VECTORSBOOK - AAKASH SERIESCHAPTER - VECTORSEXERCISE - Lecture Sheet (Exercise-I) (Integer Type Questions)
3 Videos
- UNITS AND MEASUREMENTS BOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTS EXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED))
14 Videos
- VISCOSITY BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers
3 Videos
Similar Questions
From figure the correct relation is
View SolutionFour forces of magnitudes P, 2P, 3p and 4P act along the four sides of a square ABCD in cyclic order. If the magnitude and direction of their resultant is n√2Pand15n find the value of n
View SolutionTwo clocks are being tested against a standard clock located in a national laboratory At 12 : 00 : 00 noon by standard clock, the readins of the two clocks are
DayClock - IClock - IIMonday12:00:0510:15:06Tuesday12:01:1510:14:59Wednesday11:59:0810:15:18Thursday12:01:5010:15:07Thursday12:01:5010:15:07Friday11:59:1510:14:53Saturday12:01:3010:15:24Sunday12:01:1910:15:11
From the Observations carefully read the following conclusive statements.
Statement I : Zero - error in clock II is much longer than zero - error in clock I.
Statement II : Zero - error can always be corrected by applying necessary corrective measures
Statement III : Precision of clock - I is more than precision of clock - II
Statement IV : Precision of clock - II is more than precision of clock - I
Pick up the correction option from the following.
View SolutionAn iron sphere of mass 20×10−3 kg falls through a viscous liquid with terminal velocity 0.5 m/sec. Find the terminal velocity of another iron sphere of mass 54×10−2 kg.
View SolutionDeltaABC be an equilateral triangle whose orthocentre is the origin 'O' . If bar (OA)=bar a.bar (OB)=bar b then bar (OC) is
View SolutionDeltaABC be an equilateral triangle whose orthocentre is the origin 'O' . If bar (OA)=bar a.bar (OB)=bar b then bar (OC) is
View SolutionOABCD is a pyramid with square base ABCD such that bar(OA),bar(OB),bar(OC),bar(OD) are unit vectors and bar(OA) , bar(OB) = bar(OB) .bar(OC) = bar(OC) . bar(OD) = bar(OD) . bar(OA) =1/2, then volume of the pyramid is
View SolutionThe resultant of the three vectors ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC shown in figure :-
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R01_E02_023_Q01.png" width="80%"gt
View Solutionतीन वेक्टर −−→OA,−−→OB तथा −−→OC दिखाए गए है। वृत्त कि त्रिज्या R है। तीनो वेक्टरो का परिणामी निकले।
View SolutionIf diagonals of a parallelogram ABCD intersect each other in M, then ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC+¯¯¯¯¯¯OD =
View SolutionOABC is a parallelogram. If ¯¯¯¯¯¯OA=¯a,¯¯¯¯¯¯OC=¯c find the vector equation of the side ¯¯¯¯¯¯BC.
View SolutionThe three vectors bar(OA), bar(OB) and bar(OC) have the same magnitude R. Then the sum of these vectors have magnitude.
View Solutionयदि ¯¯¯¯¯¯OA=a,¯¯¯¯¯¯OB=−b तथा C,¯¯¯¯¯¯AB पर एक ऐसा बिंदु है की ¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB तो सदिश ¯¯¯¯¯¯OC बराबर है-
View SolutionOABC సమాంతర చతుర్భుజంలో ¯¯¯¯¯¯OA=¯a, ¯¯¯¯¯¯OC=¯c, అయితే ¯¯¯¯¯¯BC రేఖ సదిశా సమీకరణాన్ని కనుక్కోండి.
View SolutionOABC is a tetrahedron D and E are the mid points of the edges ¯¯¯¯¯¯OAand¯¯¯¯¯¯BC. Then the vector ¯¯¯¯¯¯DE in terms of ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC.
View Solution
