OABCD is a pyramid with square base ABCD such that ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB,¯¯¯¯¯¯OC,¯¯¯¯¯¯OD are unit vectors and ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB=¯¯¯¯¯¯OB.¯¯¯¯¯¯OC=¯¯¯¯¯¯OC.¯¯¯¯¯¯OD=¯¯¯¯¯¯OD.¯¯¯¯¯¯OA=12, then volume of the pyramid is
Step by step video solution for OABCD is a pyramid with square base ABCD such that bar(OA),bar(OB),bar(OC),bar(OD) are unit vectors and bar(OA) , bar(OB) = bar(OB) .bar(OC) = bar(OC) . bar(OD) = bar(OD) . bar(OA) =1/2, then volume of the pyramid is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
यदि ¯¯¯¯¯¯OA=a,¯¯¯¯¯¯OB=−b तथा C,¯¯¯¯¯¯AB पर एक ऐसा बिंदु है की ¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB तो सदिश ¯¯¯¯¯¯OC बराबर है-
View SolutionThe resultant of the three vectors bar(OA), bar(OB) and bar(OC) has magnitude (R = Radius of the circle)
View SolutionOABC is a tetrahedron D and E are the mid points of the edges ¯¯¯¯¯¯OAand¯¯¯¯¯¯BC. Then the vector ¯¯¯¯¯¯DE in terms of ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC.
View SolutionIf O is the circumcentre, 'H' is the orthocentre of triangle ABC, then show that
¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC=¯¯¯¯¯¯OH
View SolutionΔABC be an equilateral triangle whose orthocentre is the origin 'O'. If ¯¯¯¯¯¯OA=¯a,¯¯¯¯¯¯OB=¯b then ¯¯¯¯¯¯OC is
View SolutionABCD is a quadrilateral. E is the point of intersection of the line joining the middle points of the opposite sides. If O is any point then ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC+¯¯¯¯¯¯OD=
View SolutionIf OABC, OCDE, OEFA are adjacent faces of a cube OABCDEF then ¯¯¯¯¯¯OB+¯¯¯¯¯¯OD+¯¯¯¯¯¯OF interms of ¯¯¯¯¯¯OA,¯¯¯¯¯¯OE,¯¯¯¯¯¯OC is
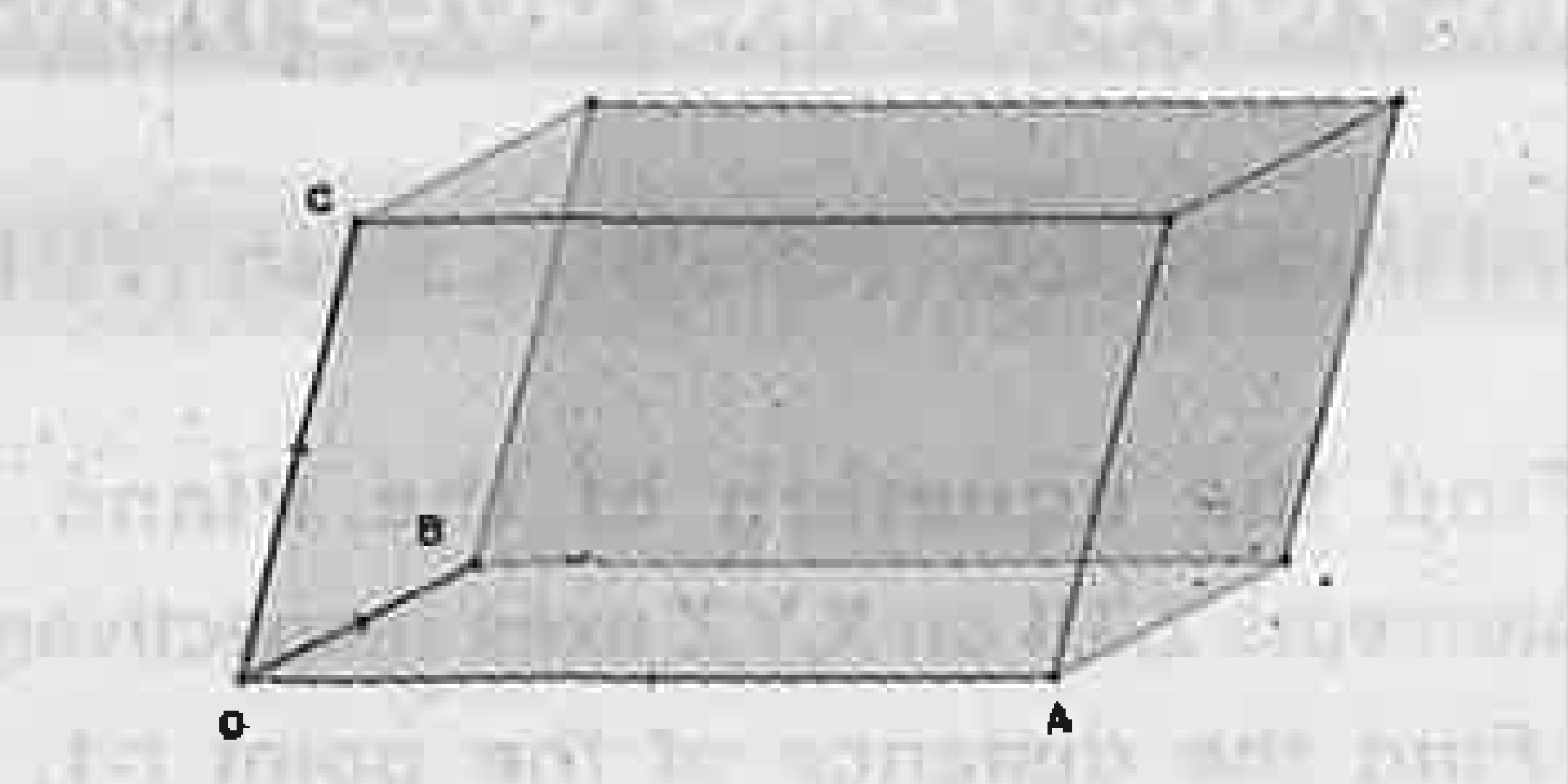
View Solution¯¯¯¯¯¯OA=i+2j+3k
¯¯¯¯¯¯OB=i−2j+4k
¯¯¯¯¯¯OC=2i+3j+k
are adjacent sides of the parallelopiped.
Find the base area of the parallelopiped.
(Base determined by ¯¯¯¯¯¯OA and ¯¯¯¯¯¯OB)
View Solution
