Two point charges q1andq2 are placed at (0, 0,0) and (1,2,2)m respectively. The repel each other with force of 3N. The force on q2 due to q1 is F21=(xˆi+yˆj+zˆk)N. Find the value of x+y+z
The correct Answer is:5
Topper's Solved these Questions
- VECTORSBOOK - AAKASH SERIESCHAPTER - VECTORSEXERCISE - Additional Practice Exercise (Practice Sheet (Advanced)) (More than one correct answer type Questions)
3 Videos
- VECTORSBOOK - AAKASH SERIESCHAPTER - VECTORSEXERCISE - Additional Practice Exercise (Practice Sheet (Advanced)) (Linked Comprehension Type Questions)
2 Videos
- VECTORSBOOK - AAKASH SERIESCHAPTER - VECTORSEXERCISE - Additional Practice Exercise (Level-II Lecture Sheet (Advanced)) (More than one correct answer Type Questions)
1 Videos
- UNITS AND MEASUREMENTS BOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTS EXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED))
14 Videos
- VISCOSITY BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers
3 Videos
Similar Questions
Knowledge Check
The vectors ˆi−2xˆj−3yˆkandˆi+3xˆj+2yˆk are orthogonal to each other. Then, the locus of the point (x, y) is:
AHyperbolaBEllipseCParabolaDCircleTwo particles P and Q are moving with velocity of (ˆi+ˆj) and (−ˆi+2ˆj) respectively. At time t=0, P is at origin and Q is at a point with positive vector (2ˆi+ˆj). Then the shortest distance between P & Q is :-
A2√55B4√55C√5D3√55
A positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
View SolutionA spherical shell having charge +Q (uniformly distributed) and a point charge +q0 are placed as shown. Find the force between shell and the point charge (r>>R).
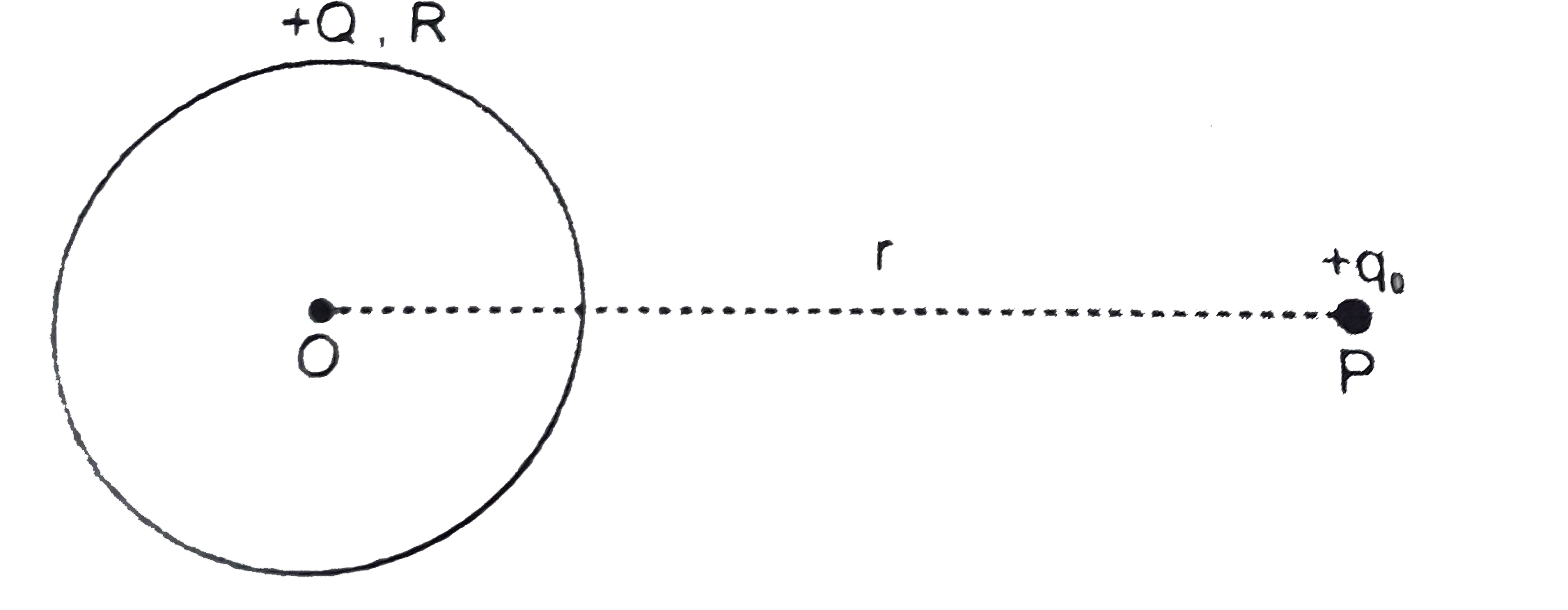
(i) Force on the point charge +q0 due to the shell =q→E0 shell=(q0)(KQr2)ˆr=KQq0r2ˆr where ˆr. is unit vector along OP.
From action - reaction principle, force on the shell due to the point charge will also be : Fshell=KQq0r2(−ˆr)
Conslusion : To find the force on a hollow sphere due to outside charges, we can replace the sphere by a point charge kept at centre.
View SolutionObtain the condition for the two vectors →A=x1ˆi+y1ˆj+z1ˆkand→B=x2ˆi=x2ˆi+y2ˆj+z2ˆk to be parallel ?
View SolutionTwo particles P and Q are moving with velocity of (ˆi+ˆj) and (−ˆi+2ˆj) respectively. At time t=0, P is at origin and Q is at a point with positive vector (2ˆi+ˆj). Then the shortest distance between P & Q is :-
View SolutionCharge q1=+6.0nC is on y-axis at y=+3cm and charge q2=−6.0nC is on y-axis at y=−3cm. Calculate force on a test charge q0=2nC placed on X-axis at x=4cm.
View SolutionThe position vectors of the points PandQ with respect to the origin O are →a=ˆi+3ˆj−2ˆk and →b=3ˆi−ˆj−2ˆk, respectively. If M is a point on PQ, such that OM is the bisector of ∠POQ, then →OM is a. 2(ˆi−ˆj+ˆk) b. 2ˆi+ˆj−2ˆk c. 2(−ˆi+ˆj−ˆk) d. 2(ˆi+ˆj+ˆk)
View Solution
