A positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
To find the force acting on the charge q1 located at (a,0) due to another charge q2 located at (0,a), we can follow these steps:
Step 1: Determine the distance between the charges
The distance r between the two charges can be calculated using the distance formula:
r=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of q1 and q2:
r=√(0−a)2+(a−0)2=√a2+a2=√2a2=a√2
Step 2: Calculate the force between the charges
Using Coulomb's law, the magnitude of the force F between two point charges is given by:
F=k|q1q2|r2
Substituting r=a√2:
F=kq1q2(a√2)2=kq1q22a2
Step 3: Determine the direction of the force
The force F acting on q1 due to q2 will be directed along the line joining the two charges. The angle θ between the line connecting the charges and the x-axis can be calculated as:
tan(θ)=y2−y1x2−x1=a−00−a=−1
Thus, θ=45∘.
Step 4: Resolve the force into components
The force F can be resolved into its x and y components:
- The x-component Fx:
Fx=Fcos(45∘)=kq1q22a2⋅1√2=kq1q22√2a2
- The y-component Fy:
Fy=Fsin(45∘)=kq1q22a2⋅1√2=kq1q22√2a2
Since the force q2 is also positive, it will repel q1 in the direction opposite to the y-axis, thus:
Fy=−kq1q22√2a2
Step 5: Write the force vector
Combining the components, the force vector →Fq1 acting on q1 is:
→Fq1=Fx^i+Fy^j=kq1q22√2a2^i−kq1q22√2a2^j
Final Result
Thus, the force acting on q1 is:
→Fq1=kq1q22√2a2(^i−^j)
The distance r between the two charges can be calculated using the distance formula:
r=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of q1 and q2:
r=√(0−a)2+(a−0)2=√a2+a2=√2a2=a√2
Using Coulomb's law, the magnitude of the force F between two point charges is given by:
F=k|q1q2|r2
Substituting r=a√2:
F=kq1q2(a√2)2=kq1q22a2
The force F acting on q1 due to q2 will be directed along the line joining the two charges. The angle θ between the line connecting the charges and the x-axis can be calculated as:
tan(θ)=y2−y1x2−x1=a−00−a=−1
Thus, θ=45∘.
The force F can be resolved into its x and y components:
- The x-component Fx:
Fx=Fcos(45∘)=kq1q22a2⋅1√2=kq1q22√2a2
- The y-component Fy:
Fy=Fsin(45∘)=kq1q22a2⋅1√2=kq1q22√2a2
Fy=−kq1q22√2a2
Combining the components, the force vector →Fq1 acting on q1 is:
→Fq1=Fx^i+Fy^j=kq1q22√2a2^i−kq1q22√2a2^j
Thus, the force acting on q1 is:
→Fq1=kq1q22√2a2(^i−^j)
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - TRY YOURSELF
33 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - ASSIGNMENT(SECTION-A) Objective Type Question
45 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
15 Videos
Similar Questions
A conducting spherical shell is earthed. A positive charge +q1 is placed at the center and another small positive charge +q2 is placed at a distance r from q1. Ignore the effect of induced charge due to q2 on the sphere. Then the coulomb force on q2 is
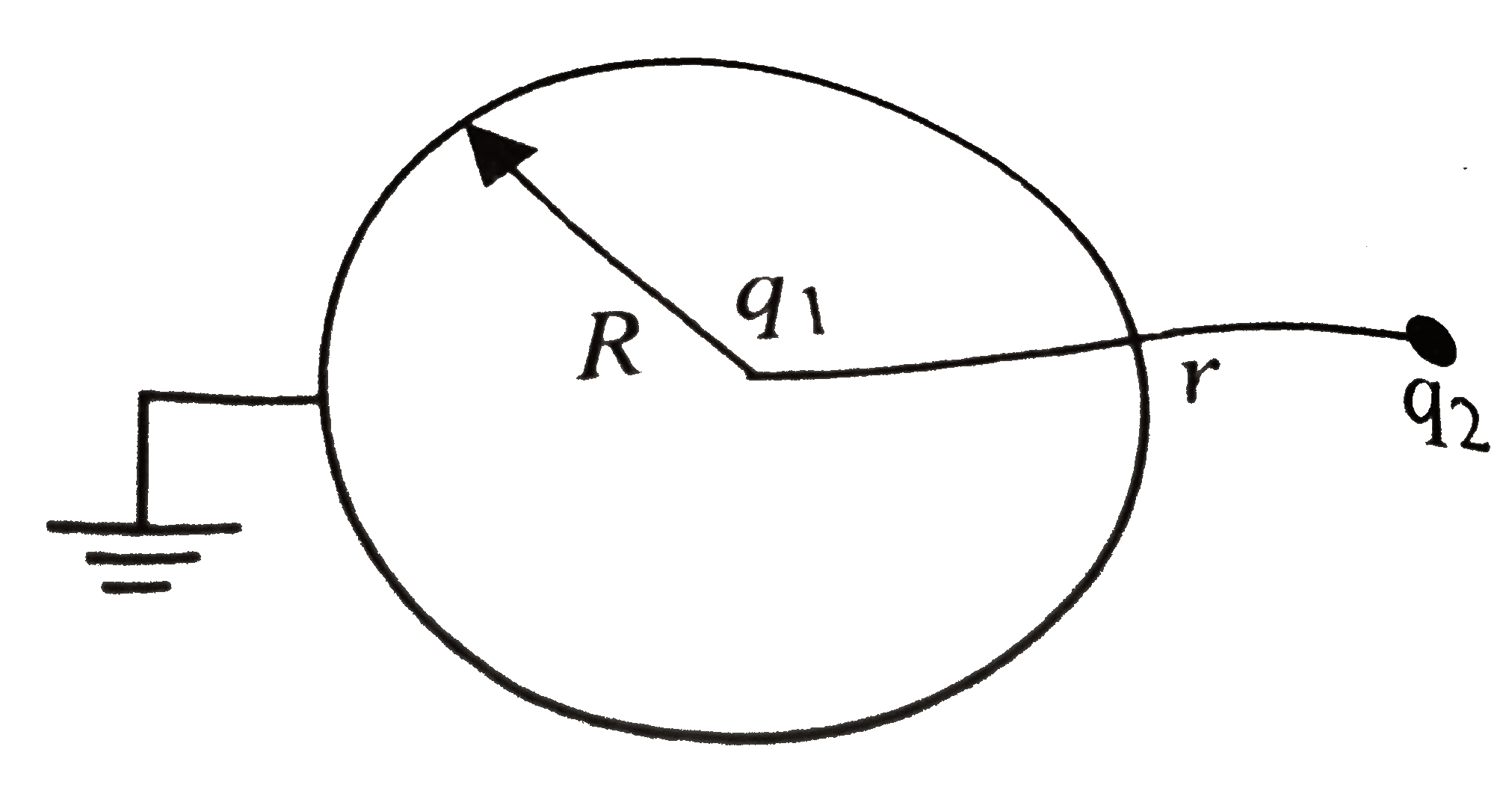
View SolutionA point charge qA=+100μc is placed at point A (1, 0, 2) m and another point charge qB=+200μc is placed at point B (4, 4, 2) m. Find :
(i) Magnitude of electrostatic interaction force acting between them
(ii) Find →FA (force on A due to B) and →FB (force on due to A) in vector form
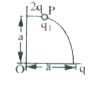
View SolutionTwo point charges q AND 2q are placed at (a,0) and (0,a) A point charge q1 is placed at a P on the quarter circle of radius a as shown in the diagram so that the electric field at the origin becomes zero
View SolutionTwo equal positive point charges 'Q' are fixed at points B (a, 0) and A(-a, 0). Another test charge q0 is also placed at O (0, 0). Show that the equilibrium at 'O' is
(i) Stable for displacement along X-axis
(ii) Unstable for displacement along Y-axis.
View SolutionA point charge q1 is placed inside cavity 1 and another point charge q2 is inside cavity 2. A point charge q is placed outside the conductor. For the situation described above, answer the following questions.

The charge on outer surface of the conductor would be
View SolutionA point charge q1 is placed inside cavity 1 and another point charge q2 is inside cavity 2. A point charge q is placed outside the conductor. For the situation described above, answer the following questions.
If the potential of the conductor is V0 and charge q2 is placed at the center of cavity 2, then potential at point Q is
View SolutionA point charge q1 is placed inside cavity 1 and another point charge q2 is inside cavity 2. A point charge q is placed outside the conductor. For the situation described above, answer the following questions.
If charge q2 is at point Q (inside cavity 2), then →E at the center of cavity 2 due to induced charge on the surface of cavity 2 would be
View SolutionA point charge q1 is placed inside cavity 1 and another point charge q2 is inside cavity 2. A point charge q is placed outside the conductor. For the situation described above, answer the following questions.
→E inside the conductor at point S distant r from point charge q, due to charge on outer surface of the conductor, would be
View SolutionElectric potential is a scalar quantity. Due to a point charge charge q at distance r, the potential is given by V=q4π∈0r. A point charge q is placed at (3a,0) and another charge −2q is placed at (−3a,0).
At how many points on the x-axis, (at finite distance) electric potential will be zero?
View SolutionInside a neutral hollow conducting sphere of radius X and centre C, a point charge q is placed as shown in the figure. Another point charge q1, is placed outside the sphere at distance d from centre. The net- electrostatic force on charge q placed at the centre is K=14πε0

View Solution