An YDSE is carried out in a liquid of refractive index μ=1.3 and thin film of air is formed in from of the lower slit as shown in the figure.
In the above problem find the distance of fourth maxima from 0.
β=λDμd=0.781.3×10−6×103=0.6mm
Shift in the fringe pattern will be upwards
The refrective index of the air film is less than the medium Find the maxima ⇒:0.6mm below 0
∴−0.6mm
∴7×0.6mm=4.2mm above 0
The fourth maxima are 4.2mm above 0 and 0.6mm below 0.
Topper's Solved these Questions
Similar Questions
In the above problem the displacement after 2 s is:
View SolutionYDSE is carried out in a liquid of refractive index μ=1.3 and a thin film of air is formed in front of the lower slit as shown in the figure. If a maxima of third order is formed at the origin O, find the thickness of the air film. Find the positions of the fourth maxima. The wavelength of light is air is λ0=0.78μm and D/d=1000.
View Solution
Knowledge Check
In a regular YDSE, when thin film of refractive index mu is placed in front of the upper slit then it is observed that the intensity at the central point becomes half of the original intensity. It is also observed that the initial 3^(rd) maxima is now below the central point and the initial 4th minima is above the central point. Now, a film of refractive index μ1 and thickness same as the above film. is put in the front of the lower slit also. It is observed that whole fringe pattern shifts by one fringe width. What is the value of μ1 ?
A(4μ+9)/12B(4μ+9)/13C(4μ+9)/11DNoneA YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)

Now, if 600 nm, find the wavelength of the ligth that forms maximum exactly at point O.A650 nm, 433.3 nmB550 nm, 750 nmC450 nm, 645.3 nmD375 nm, 525.3 nm
Two transparent sheets of thickness t1 and t2 and refractive indexes μ1 and μ2 are placed infront of the slits in YDSE setup as shown in figure-6.47. If D is the distance of the screen from the slits, then find the distance of zero order maxima from the centre of the screen. What is the condition that zero order maxima is formed at the centre O?

[D[(μ1−1)t1−(μ2−1)t2]d,(μ2−1)t2]
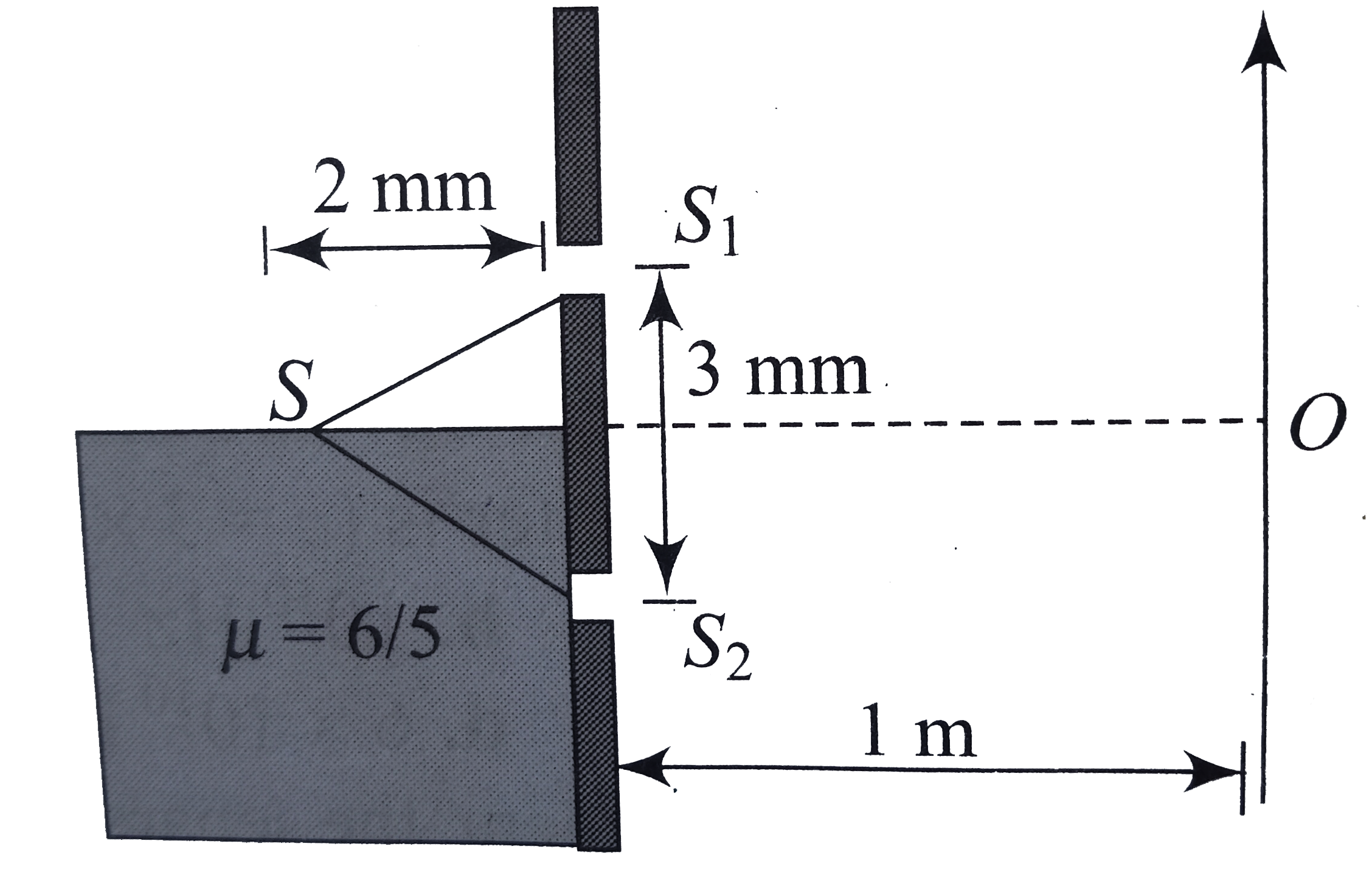
View SolutionIn Young's double-slit experiment, a point source is placed on a solid slab of refractive index 6/5 at a distance of 2 mm from two slits spaced 3 mm apart as shown and at equal distacne from both the slits. The screen is at a distance of 1 m from the slits. Wavelength of light used is 500 nm.
a. Find the position of the central maximum.
b. Find the order of the fringe formed at O.
c. A film of refractive index 1.8 is to be placed in front of S1 so that central maxima is formed where 200th maxima was formed. Find the thickness of film.
View SolutionIn Young's double-slit experiment, a point source is placed on a solid slab of refractive index 6/5 at a distance of 2 mm from two slits spaced 3 mm apart as shown and at equal distance from both the slits. The screen is at a distance of 1 m from the slits. Wavelength of light used is 500 nm.
a. Find the position of the central maximum.
b. Find the order of the fringe formed at O.
c. A film of refractive index 1.8 is to be placed in front of S1 so that central maxima is formed where 200th maxima was formed. Find the thickness of film.

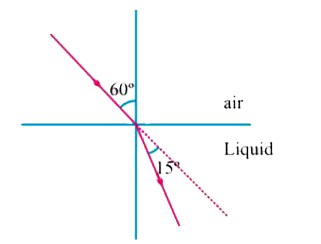
View SolutionA light ray passes from air into a liquid as shown in figure. Find refractive index of liquid.
View SolutionA YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)

Now, if 600 nm, find the wavelength of the ligth that forms maximum exactly at point O.
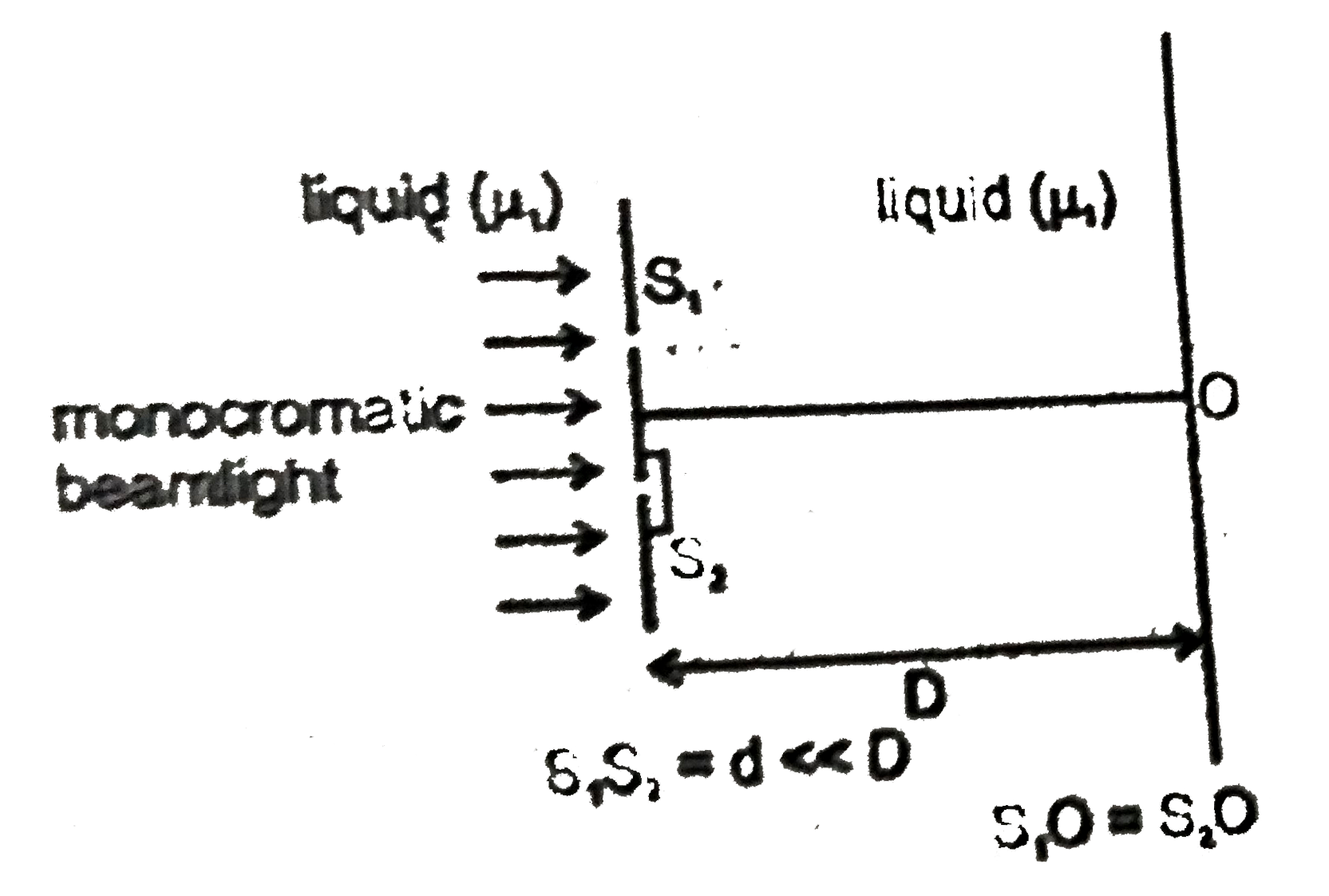
View SolutionYoung's double slit experiment is conducted in a liquid of refractive index μ1 as shown in figure. A thin transparent slab of refractive index μ2 is placed in front of the slit s2. The magnitude of optical path difference at 'O' is
View Solution
