A cube of side 1 is placed in a uniform field E, where E=Eˆi. The net electric flux through the cube is
zero
12E
412E
612E
The correct Answer is:A
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBook:AAKASH SERIESChapter:ELECTRIC CHARGES AND FIELDSExercise:Exercise-II
Explore 56 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:AAKASH SERIESChapter:DUAL NATURE OF RADIATION AND MATTERExercise:PRACTICE EXERCISEX
Explore 44 Videos
- ELECTRIC FIELD AND POTENTIALBook:AAKASH SERIESChapter:ELECTRIC FIELD AND POTENTIALExercise:PROBLEMS (LEVEL-II)
Explore 32 Videos
Similar Questions
Knowledge Check
A cube of side l is placed in a uniform field E, where E= Eˆi .The net electric flux through the cube is
AzeroBl2EC4l2ED6l2EA cube of side l is p laced in a uniform field E, where E=Eˆi. The net electric flux through the cube is
AzeroBl2EC4l2ED6l2EA hemispherical bowl of radius r is placed in uniform electric field E . The electric flux passing through the bowl is
Aπr2EB2πrE2C4πr2ED4πrE2
A cube has sides of length L=0.2 m It is placed with one corner at the origin as shown in figure The electric field in uniform and given by →E=(2.5ˆi−4.2ˆj)N/C .Find the electric flux through the entire cube.

View SolutionState Gauss’s law in electrostatics. A cube with each side a is kept in an electric field given by E = Cx (as shown in the figure) where C is a positive dimensional constant. Find out :
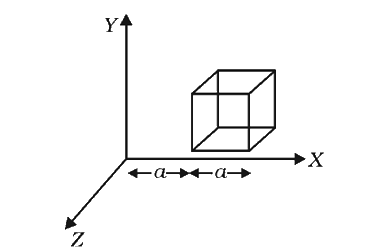
(i) The electric flux through the cube (ii) The net charge inside the cube.
View SolutionA cube has sides of length L=0.2m. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=(2.5N/C)ˆi−(4.2N/C)ˆj. Find the electric flux through the entire cube.
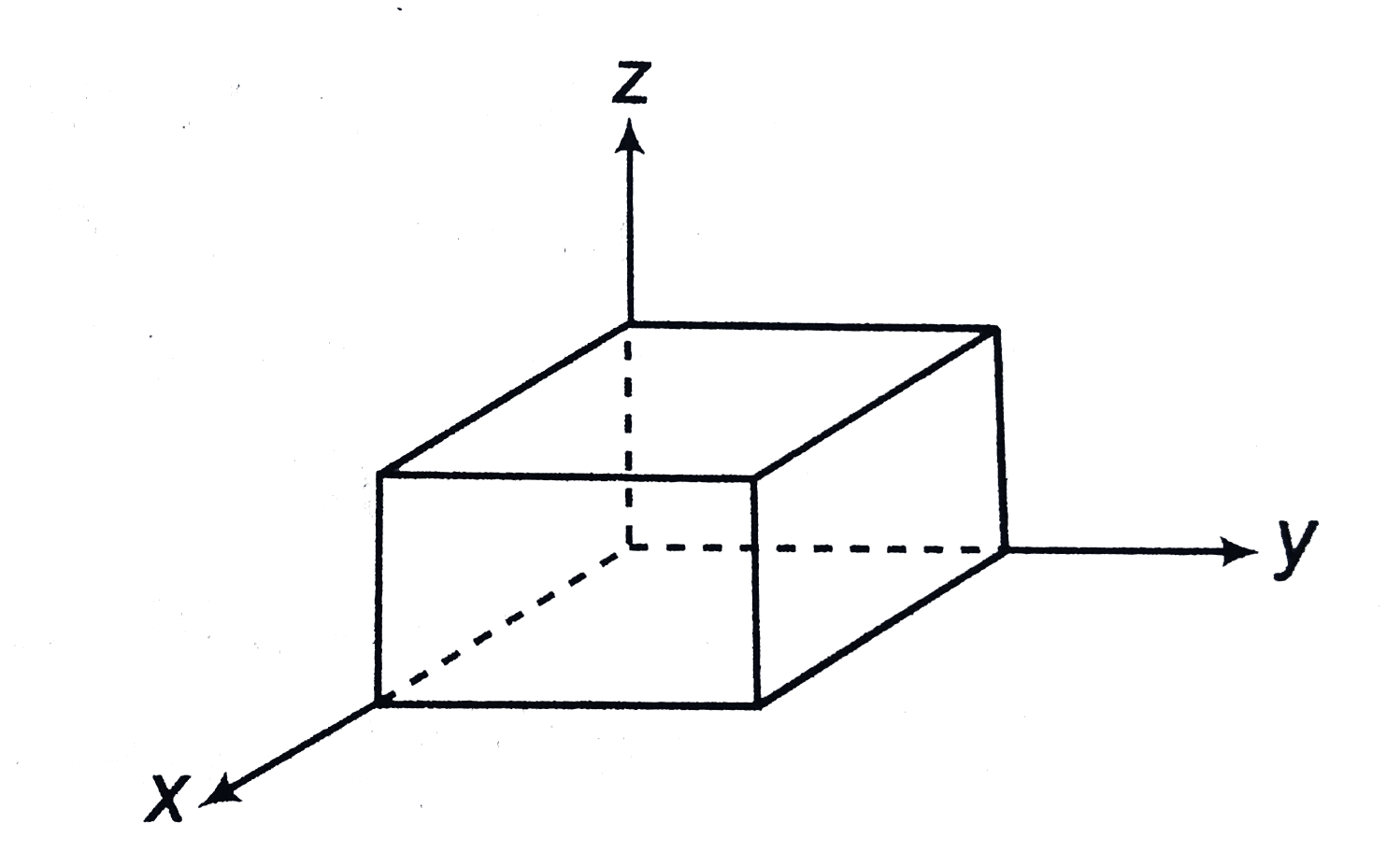
View SolutionA cube has sides of length L=0.2m. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=(2.5N/C)ˆi−(4.2N/C)ˆj. Find the electric flux through the entire cube.

View SolutionA cube of side a is placed in a uniform electric field E=E0ˆi+E0ˆj+E0ˆk. Total electric flux passing through the cube would be
View Solution