A cube of side a is placed in a uniform electric field E=E0ˆi+E0ˆj+E0k. Total electric flux passing through the cube would be
E0a2
2E0a2
6E0a2
None of these
The correct Answer is:D
To calculate the total electric flux passing through a cube placed in a uniform electric field, we can follow these steps:
Step 1: Understand the Electric Field
The electric field is given as:
E=E0^i+E0^j+E0^k
This means the electric field has equal components in the x, y, and z directions.
Step 2: Identify the Cube's Faces
A cube has six faces. We will denote the area of each face as A=a2, where a is the side length of the cube.
Step 3: Calculate the Electric Flux Through Each Face
The electric flux Φ through a surface is given by:
Φ=E⋅A
where A is the area vector of the surface.
1. For the face perpendicular to the x-axis (front and back faces):
- Area vector for the front face: A1=a2^i
- Area vector for the back face: A2=−a2^i
- Flux through front face:
Φ1=E⋅A1=(E0^i+E0^j+E0^k)⋅(a2^i)=E0a2
- Flux through back face:
Φ2=E⋅A2=(E0^i+E0^j+E0^k)⋅(−a2^i)=−E0a2
- Total flux through these two faces:
Φ1+2=E0a2−E0a2=0
2. For the face perpendicular to the y-axis (left and right faces):
- Area vector for the left face: A3=−a2^j
- Area vector for the right face: A4=a2^j
- Flux through left face:
Φ3=E⋅A3=(E0^i+E0^j+E0^k)⋅(−a2^j)=−E0a2
- Flux through right face:
Φ4=E⋅A4=(E0^i+E0^j+E0^k)⋅(a2^j)=E0a2
- Total flux through these two faces:
Φ3+4=−E0a2+E0a2=0
3. For the face perpendicular to the z-axis (top and bottom faces):
- Area vector for the bottom face: A5=−a2^k
- Area vector for the top face: A6=a2^k
- Flux through bottom face:
Φ5=E⋅A5=(E0^i+E0^j+E0^k)⋅(−a2^k)=−E0a2
- Flux through top face:
Φ6=E⋅A6=(E0^i+E0^j+E0^k)⋅(a2^k)=E0a2
- Total flux through these two faces:
Φ5+6=−E0a2+E0a2=0
Step 4: Calculate Total Electric Flux
Now, adding the flux through all six faces:
Φtotal=Φ1+2+Φ3+4+Φ5+6=0+0+0=0
Final Answer
The total electric flux passing through the cube is:
Φtotal=0
The electric field is given as:
E=E0^i+E0^j+E0^k
This means the electric field has equal components in the x, y, and z directions.
A cube has six faces. We will denote the area of each face as A=a2, where a is the side length of the cube.
The electric flux Φ through a surface is given by:
Φ=E⋅A
where A is the area vector of the surface.
- Area vector for the front face: A1=a2^i
- Area vector for the back face: A2=−a2^i
Φ1=E⋅A1=(E0^i+E0^j+E0^k)⋅(a2^i)=E0a2
Φ2=E⋅A2=(E0^i+E0^j+E0^k)⋅(−a2^i)=−E0a2
Φ1+2=E0a2−E0a2=0
- Area vector for the left face: A3=−a2^j
- Area vector for the right face: A4=a2^j
Φ3=E⋅A3=(E0^i+E0^j+E0^k)⋅(−a2^j)=−E0a2
Φ4=E⋅A4=(E0^i+E0^j+E0^k)⋅(a2^j)=E0a2
Φ3+4=−E0a2+E0a2=0
- Area vector for the bottom face: A5=−a2^k
- Area vector for the top face: A6=a2^k
Φ5=E⋅A5=(E0^i+E0^j+E0^k)⋅(−a2^k)=−E0a2
Φ6=E⋅A6=(E0^i+E0^j+E0^k)⋅(a2^k)=E0a2
Φ5+6=−E0a2+E0a2=0
Now, adding the flux through all six faces:
Φtotal=Φ1+2+Φ3+4+Φ5+6=0+0+0=0
The total electric flux passing through the cube is:
Φtotal=0
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Taking it together
105 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.4
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Knowledge Check
The potential field of an electric field →E=(yˆi+xˆj) is
AV = -(x+y) + constantBV = constantCV=−(x2+y2)+ constantDV = -xy + constant
The potential field of an electric field →E=(yˆi+xˆj) is
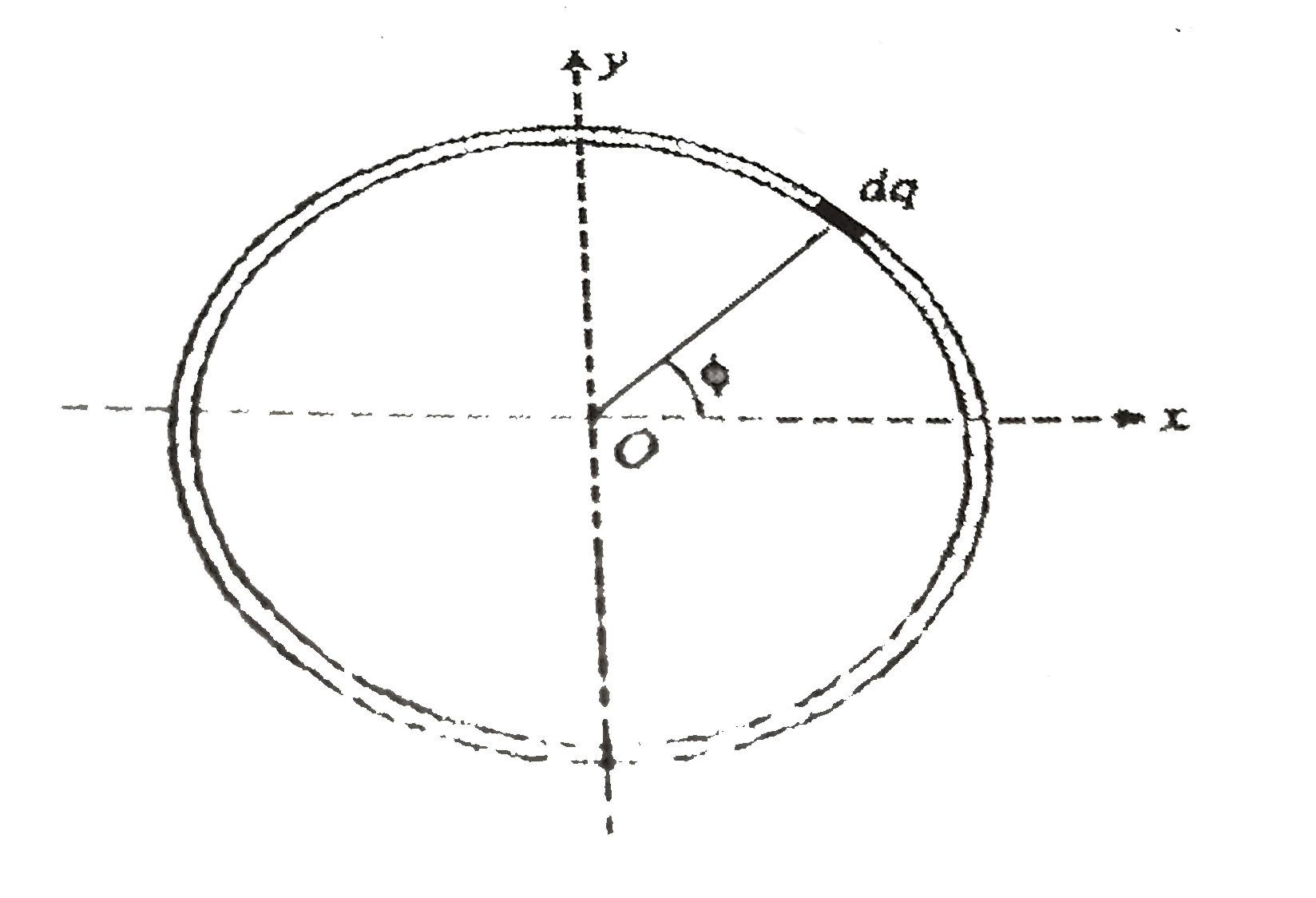
View SolutionA thin non-conducting ring or radius a has a linear charge density λ=λ0sinϕ. A uniform electric field E0ˆi+E0ˆj exist in the region . .Net torque acting on ring is given as :
View SolutionA square of side 'a' is lying in xy plane such that two of its sides are lying on the axis. If an electric field →E=E0xˆk is applied on the square. The flux passing through the square is :
View SolutionA cube has sides of length L=0.300m. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by →E=(−5.00NC−1)xˆi+(3.00NC−1)zˆk.
The flux passing through the surface S5 will be
View SolutionIf the electric field is given by 3ˆi+2ˆj+6ˆk . Find the electric flux through a surface area 20 unit lying in xy plane
View SolutionThe electric field in a region of space is given by, →E=E0ˆi+2E0ˆj where E0=100N/C. The flux of this field through a circular surface of radius 0.02m parallel to the Y-Z plane is nearly.
View SolutionThe electric field in a region is given by →E=E0axˆi. Find the electric flux passing through a cubical volume bounded by the surfaces x=0,x=a,y=0,y=a,z=0 and z=a.
View Solution
