If V0 be the potential at origin in an electric field Qπε0R the potential at (x,y) is
V0−xEx−yEy
V0+xEx+yEy
xEx+yEy−V0
√x2+y2√E2x+E2y−Vo
The correct Answer is:A
Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - LECTURE SHEET (EXERCISE - IV) (LEVEL - II (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
4 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - LECTURE SHEET (EXERCISE - IV) (LEVEL - II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
3 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - LECTURE SHEET (EXERCISE - IV) (LEVEL - I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
10 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
6 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
9 Videos
Similar Questions
Knowledge Check
Let V0 be the potential at the origin in an electric field →E=Exˆi+Eyˆj. The potential at the point (x,y) is
AV0−xEx−yEyBV0+xEx+yEyCxEx+yEy−V0D(√x2+y2)√E2x+E2y−V0Let V0 be the potential at the origin in an electric field →E=4ˆi+5ˆj. The potential at the point (x,y) is
AV0−4x−5yBV0+4x+5yC4x+5y−V0D−4x−5yAssume that an electric field →E=30x2ˆi exists in space. Then the potentail differences VA−V0 where V0 is the potential at the origin and VA, the potebntail at x=2m is
A−80VB80VC120VD−120V
Assume that an electric field →E=30x2ˆi exists in space. Then the potential differences VA−V0 where V0 is the potential at the origin and VA, the potential at x=2m is
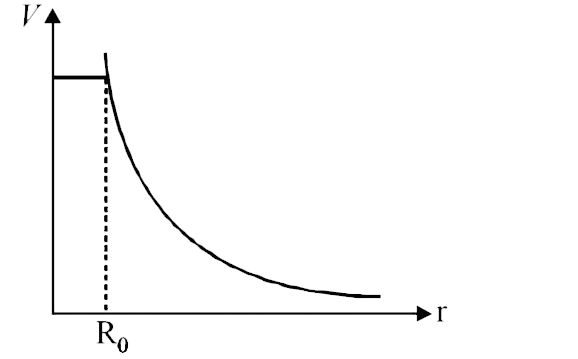
View SolutionA spherical symmetric charge system is centered at origin. Given, Electric potential
V=Q4πε0R0(r≤R0), V=Q4πε0r(r>R0)
View SolutionA charge +q is fixed at each of the points x=x0, x=3x0, x=5x0,…………x=∞ on the x axis, and a charge −q is fixed at each of the points x=2x0, x=4x0, x=6x0, …………x=∞. Here x0 is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be Q/(4πε0r).Then, the potential at the origin due to the above system of
View SolutionA spherical symmetric charge system is centered at origin. Given, Electric potential
V=Q4πε0R0(r≤R0), V=Q4πε0r(r>R0)

View SolutionA charge +q is fixed at each of the points x=x0, x=3x0, x=5x0,…………x=∞ on the x axis, and a charge −q is fixed at each of the points x=2x0, x=4x0, x=6x0, …………x=∞. Here x0 is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be Q/(4πε0r).Then, the potential at the origin due to the above system of
View Solution
